25秋深度学习训练营-第2周：卷积神经网络

9 minute read

第2周：卷积神经网络

学习内容：https://oucai.club/classes/dl/week01#第2周-卷积神经网络

学习视频：https://www.jianguoyun.com/p/Dde3HS8QrKKIBhi2xpEGIAA

视频学习至1小时06分，包括：

CNN的基本结构：卷积、池化、全连接

代码练习

实验1: 使用 LeNet 对 MNIST 数据集分类

Epoch [1/10], Step [100/938], Loss: 0.9421, Accuracy: 70.53%
Epoch [1/10], Step [200/938], Loss: 0.2978, Accuracy: 80.96%
Epoch [1/10], Step [300/938], Loss: 0.1998, Accuracy: 85.28%
Epoch [1/10], Step [400/938], Loss: 0.1483, Accuracy: 87.91%
Epoch [1/10], Step [500/938], Loss: 0.1318, Accuracy: 89.54%
Epoch [1/10], Step [600/938], Loss: 0.1123, Accuracy: 90.72%
Epoch [1/10], Step [700/938], Loss: 0.0962, Accuracy: 91.64%
Epoch [1/10], Step [800/938], Loss: 0.1050, Accuracy: 92.31%
Epoch [1/10], Step [900/938], Loss: 0.0876, Accuracy: 92.84%
Test Loss: 0.0854, Test Accuracy: 97.36%

Epoch [2/10], Step [100/938], Loss: 0.0724, Accuracy: 97.58%
Epoch [2/10], Step [200/938], Loss: 0.0759, Accuracy: 97.56%
Epoch [2/10], Step [300/938], Loss: 0.0701, Accuracy: 97.63%
Epoch [2/10], Step [400/938], Loss: 0.0674, Accuracy: 97.72%
Epoch [2/10], Step [500/938], Loss: 0.0710, Accuracy: 97.73%
Epoch [2/10], Step [600/938], Loss: 0.0669, Accuracy: 97.77%
Epoch [2/10], Step [700/938], Loss: 0.0625, Accuracy: 97.82%
Epoch [2/10], Step [800/938], Loss: 0.0561, Accuracy: 97.88%
Epoch [2/10], Step [900/938], Loss: 0.0608, Accuracy: 97.91%
Test Loss: 0.0484, Test Accuracy: 98.39%

Epoch [3/10], Step [100/938], Loss: 0.0442, Accuracy: 98.55%
Epoch [3/10], Step [200/938], Loss: 0.0591, Accuracy: 98.39%
Epoch [3/10], Step [300/938], Loss: 0.0406, Accuracy: 98.51%
Epoch [3/10], Step [400/938], Loss: 0.0455, Accuracy: 98.55%
Epoch [3/10], Step [500/938], Loss: 0.0498, Accuracy: 98.51%
Epoch [3/10], Step [600/938], Loss: 0.0424, Accuracy: 98.51%
Epoch [3/10], Step [700/938], Loss: 0.0452, Accuracy: 98.52%
Epoch [3/10], Step [800/938], Loss: 0.0542, Accuracy: 98.49%
Epoch [3/10], Step [900/938], Loss: 0.0410, Accuracy: 98.50%
Test Loss: 0.0415, Test Accuracy: 98.62%

Epoch [4/10], Step [100/938], Loss: 0.0353, Accuracy: 98.89%
Epoch [4/10], Step [200/938], Loss: 0.0337, Accuracy: 98.92%
Epoch [4/10], Step [300/938], Loss: 0.0398, Accuracy: 98.90%
Epoch [4/10], Step [400/938], Loss: 0.0357, Accuracy: 98.89%
Epoch [4/10], Step [500/938], Loss: 0.0416, Accuracy: 98.84%
Epoch [4/10], Step [600/938], Loss: 0.0442, Accuracy: 98.80%
Epoch [4/10], Step [700/938], Loss: 0.0336, Accuracy: 98.80%
Epoch [4/10], Step [800/938], Loss: 0.0319, Accuracy: 98.85%
Epoch [4/10], Step [900/938], Loss: 0.0400, Accuracy: 98.84%
Test Loss: 0.0440, Test Accuracy: 98.60%

Epoch [5/10], Step [100/938], Loss: 0.0287, Accuracy: 99.17%
Epoch [5/10], Step [200/938], Loss: 0.0251, Accuracy: 99.23%
Epoch [5/10], Step [300/938], Loss: 0.0291, Accuracy: 99.18%
Epoch [5/10], Step [400/938], Loss: 0.0275, Accuracy: 99.18%
Epoch [5/10], Step [500/938], Loss: 0.0351, Accuracy: 99.09%
Epoch [5/10], Step [600/938], Loss: 0.0325, Accuracy: 99.07%
Epoch [5/10], Step [700/938], Loss: 0.0320, Accuracy: 99.05%
Epoch [5/10], Step [800/938], Loss: 0.0337, Accuracy: 99.03%
Epoch [5/10], Step [900/938], Loss: 0.0245, Accuracy: 99.06%
Test Loss: 0.0468, Test Accuracy: 98.52%

Epoch [6/10], Step [100/938], Loss: 0.0277, Accuracy: 99.05%
Epoch [6/10], Step [200/938], Loss: 0.0258, Accuracy: 99.11%
Epoch [6/10], Step [300/938], Loss: 0.0264, Accuracy: 99.14%
Epoch [6/10], Step [400/938], Loss: 0.0229, Accuracy: 99.18%
Epoch [6/10], Step [500/938], Loss: 0.0194, Accuracy: 99.23%
Epoch [6/10], Step [600/938], Loss: 0.0277, Accuracy: 99.19%
Epoch [6/10], Step [700/938], Loss: 0.0233, Accuracy: 99.20%
Epoch [6/10], Step [800/938], Loss: 0.0238, Accuracy: 99.20%
Epoch [6/10], Step [900/938], Loss: 0.0288, Accuracy: 99.18%
Test Loss: 0.0554, Test Accuracy: 98.28%

Epoch [7/10], Step [100/938], Loss: 0.0193, Accuracy: 99.28%
Epoch [7/10], Step [200/938], Loss: 0.0249, Accuracy: 99.28%
Epoch [7/10], Step [300/938], Loss: 0.0211, Accuracy: 99.33%
Epoch [7/10], Step [400/938], Loss: 0.0196, Accuracy: 99.37%
Epoch [7/10], Step [500/938], Loss: 0.0257, Accuracy: 99.30%
Epoch [7/10], Step [600/938], Loss: 0.0226, Accuracy: 99.30%
Epoch [7/10], Step [700/938], Loss: 0.0212, Accuracy: 99.30%
Epoch [7/10], Step [800/938], Loss: 0.0267, Accuracy: 99.29%
Epoch [7/10], Step [900/938], Loss: 0.0181, Accuracy: 99.30%
Test Loss: 0.0441, Test Accuracy: 98.65%

Epoch [8/10], Step [100/938], Loss: 0.0145, Accuracy: 99.50%
Epoch [8/10], Step [200/938], Loss: 0.0164, Accuracy: 99.48%
Epoch [8/10], Step [300/938], Loss: 0.0179, Accuracy: 99.46%
Epoch [8/10], Step [400/938], Loss: 0.0161, Accuracy: 99.44%
Epoch [8/10], Step [500/938], Loss: 0.0165, Accuracy: 99.44%
Epoch [8/10], Step [600/938], Loss: 0.0177, Accuracy: 99.45%
Epoch [8/10], Step [700/938], Loss: 0.0211, Accuracy: 99.43%
Epoch [8/10], Step [800/938], Loss: 0.0210, Accuracy: 99.41%
Epoch [8/10], Step [900/938], Loss: 0.0194, Accuracy: 99.41%
Test Loss: 0.0316, Test Accuracy: 99.08%

Epoch [9/10], Step [100/938], Loss: 0.0100, Accuracy: 99.69%
Epoch [9/10], Step [200/938], Loss: 0.0136, Accuracy: 99.63%
Epoch [9/10], Step [300/938], Loss: 0.0176, Accuracy: 99.56%
Epoch [9/10], Step [400/938], Loss: 0.0210, Accuracy: 99.50%
Epoch [9/10], Step [500/938], Loss: 0.0144, Accuracy: 99.52%
Epoch [9/10], Step [600/938], Loss: 0.0167, Accuracy: 99.50%
Epoch [9/10], Step [700/938], Loss: 0.0228, Accuracy: 99.46%
Epoch [9/10], Step [800/938], Loss: 0.0197, Accuracy: 99.46%
Epoch [9/10], Step [900/938], Loss: 0.0136, Accuracy: 99.46%
Test Loss: 0.0403, Test Accuracy: 98.86%

Epoch [10/10], Step [100/938], Loss: 0.0097, Accuracy: 99.66%
Epoch [10/10], Step [200/938], Loss: 0.0141, Accuracy: 99.59%
Epoch [10/10], Step [300/938], Loss: 0.0089, Accuracy: 99.63%
Epoch [10/10], Step [400/938], Loss: 0.0187, Accuracy: 99.59%
Epoch [10/10], Step [500/938], Loss: 0.0182, Accuracy: 99.56%
Epoch [10/10], Step [600/938], Loss: 0.0150, Accuracy: 99.55%
Epoch [10/10], Step [700/938], Loss: 0.0113, Accuracy: 99.55%
Epoch [10/10], Step [800/938], Loss: 0.0200, Accuracy: 99.51%
Epoch [10/10], Step [900/938], Loss: 0.0195, Accuracy: 99.50%
Test Loss: 0.0391, Test Accuracy: 98.93%

Best Test Accuracy: 99.08%

经过多轮训练尝试，我们发现第十次的准确度并非最高，反而是第九次的准确度达到了99%以上

为什么不保存最后一轮的模型？

训练过程中，模型性能通常是 “提升→峰值→下降” 的趋势（过拟合）：

前几轮：模型学习训练集规律，测试准确率逐步提升；峰值轮：测试准确率达到最高（泛化能力最强）；后续轮：模型开始 “死记” 训练集（过拟合），训练准确率继续提升，但测试准确率下降。如果只保存最后一轮的模型，大概率是过拟合的模型；而保存 “最优准确率” 对应的模型，能拿到泛化能力最好的版本。

实验2：MNIST数据集分类(使用参数接近的MLP和CNN分别对MNIST数据集分类)

构建简单的CNN对mnist数据集进⾏分类。

第一步：加载数据（MNIST）

PyTorch里包含了MNIST，CIFAR10等常用数据集，调用torchvision.datasets即可把这些数据由远程下载到本地，MNIST的使用方法如下：

torchvision.datasets.MNIST(root, train=True, transform=None, target_transform=None, download=False)

root 为数据集下载到本地后的根目录，包括 training.pt 和 test.pt 文件
train，如果设置为True，从training.pt创建数据集，否则从test.pt创建。
download，如果设置为True, 从互联网下载数据并放到root文件夹下
transform, 一种函数或变换，输入PIL图片，返回变换之后的数据。
target_transform 一种函数或变换，输入目标，进行变换。

Code0

Code1

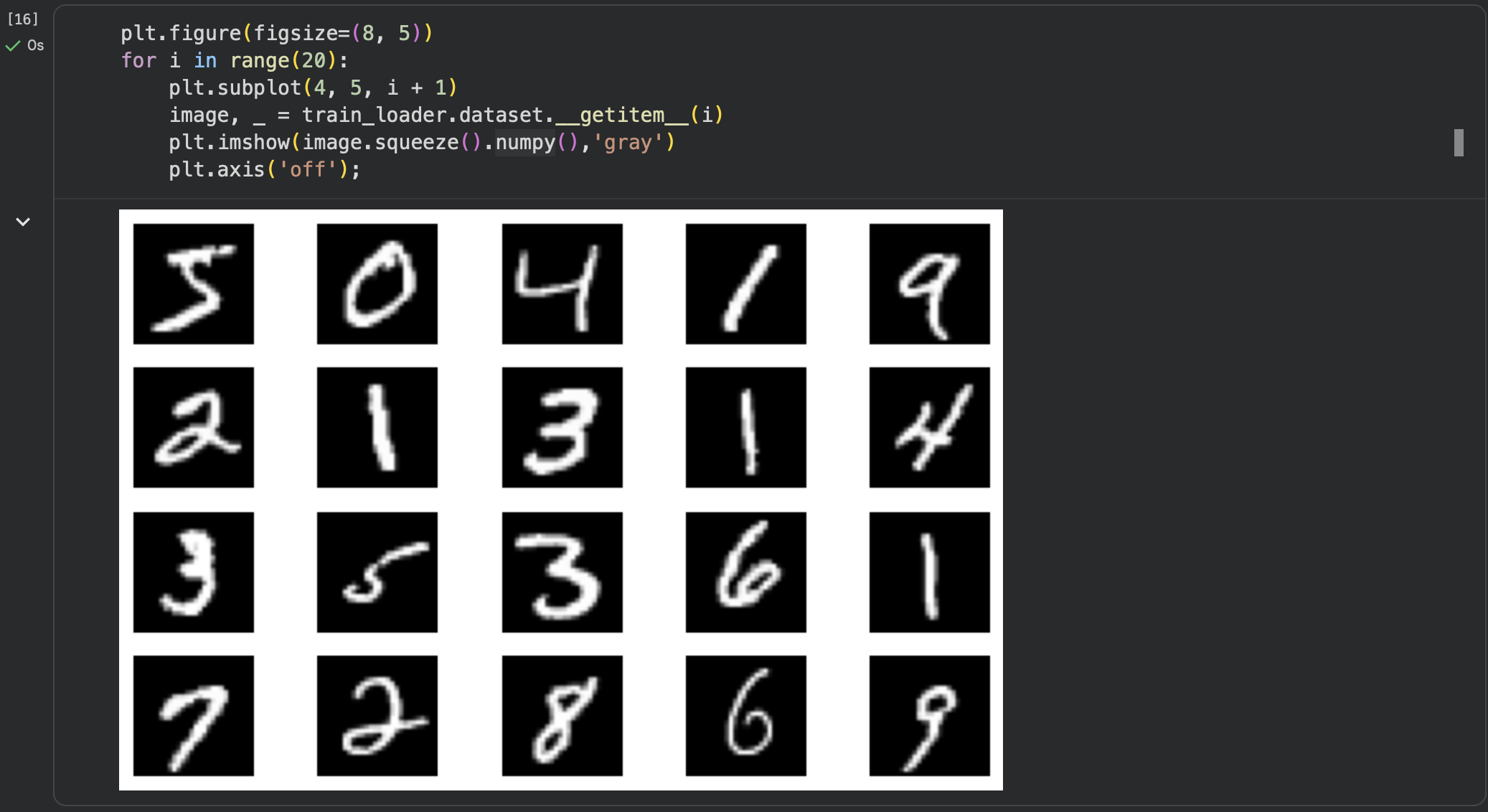
Code2

我们在从远程下载 MNIST 数据时将shuffle=True，然而在此处的20张图并没有被打乱顺序。

原因在于这里访问的是：train_loader.dataset（原始数据集 MNIST）

而shuffle发生在DataLoader的batch抓取阶段：

Code3

可以看到数据已经被打乱展示

第二步：创建网络

class FC2Layer(nn.Module):
    def __init__(self, input_size, n_hidden, output_size):
        # nn.Module子类的函数必须在构造函数中执行父类的构造函数# 下式等价于nn.Module.__init__(self)        
        super(FC2Layer, self).__init__()
        self.input_size = input_size
        # 这里直接用 Sequential 就定义了网络，注意要和下面 CNN 的代码区分开
        self.network = nn.Sequential(
            nn.Linear(input_size, n_hidden), 
            nn.ReLU(), 
            nn.Linear(n_hidden, n_hidden), 
            nn.ReLU(), 
            nn.Linear(n_hidden, output_size), 
            nn.LogSoftmax(dim=1)
        )

    def forward(self, x):
        # view一般出现在model类的forward函数中，用于改变输入或输出的形状
        # x.view(-1, self.input_size) 的意思是多维的数据展成二维
        # 代码指定二维数据的列数为 input_size=784，行数 -1 表示我们不想算，
        # 电脑会自己计算对应的数字
        # 在 DataLoader 部分，我们可以看到 batch_size 是64，所以得到 x 的行数是64
        # 大家可以加一行代码：print(x.cpu().numpy().shape)
        # 训练过程中，就会看到 (64, 784) 的输出，和我们的预期是一致的
        # forward 函数的作用是，指定网络的运行过程，这个全连接网络可能看不啥意义
        # 下面的CNN网络可以看出 forward 的作用。
        x = x.view(-1, self.input_size)
        return self.network(x)

class CNN(nn.Module):
    def __init__(self, input_size, n_feature, output_size):
        # 执行父类的构造函数，所有的网络都要这么写
        super(CNN, self).__init__()
        # 下面是网络里典型结构的一些定义，一般就是卷积和全连接
        # 池化、ReLU一类的不用在这里定义
        self.n_feature = n_feature
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=n_feature, kernel_size=5)
        self.conv2 = nn.Conv2d(n_feature, n_feature, kernel_size=5)
        self.fc1 = nn.Linear(n_feature*4*4, 50)
        self.fc2 = nn.Linear(50, 10)    
    
    # 下面的 forward 函数，定义了网络的结构，按照一定顺序，把上面构建的一些结构组织起来
    # 意思就是，conv1, conv2 等等的，可以多次重用
    def forward(self, x, verbose=False):
        x = self.conv1(x)
        x = F.relu(x)
        x = F.max_pool2d(x, kernel_size=2)
        x = self.conv2(x)
        x = F.relu(x)
        x = F.max_pool2d(x, kernel_size=2)
        x = x.view(-1, self.n_feature*4*4)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        x = F.log_softmax(x, dim=1)
        return x

# 训练函数
def train(model):
    model.train()
    # 主里从train_loader里，64个样本一个batch为单位提取样本进行训练
    for batch_idx, (data, target) in enumerate(train_loader):
        # 把数据送到GPU中
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % 100 == 0:
            print('Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))


def test(model):
    model.eval()
    test_loss = 0
    correct = 0
    for data, target in test_loader:
        # 把数据送到GPU中
        data, target = data.to(device), target.to(device)
        # 把数据送入模型，得到预测结果
        output = model(data)
        # 计算本次batch的损失，并加到 test_loss 中
        test_loss += F.nll_loss(output, target, reduction='sum').item()
        # get the index of the max log-probability，最后一层输出10个数
        # 值最大的那个即对应着分类结果，然后把分类结果保存在 pred 里
        pred = output.data.max(1, keepdim=True)[1]
        # 将 pred 与 target 相比，得到正确预测结果的数量，并加到 correct 中
        # 这里需要注意一下 view_as ，意思是把 target 变成维度和 pred 一样的意思                                                
        correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()

    test_loss /= len(test_loader.dataset)
    accuracy = 100. * correct / len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        accuracy))

第三步：在小型全连接网络上训练（Fully-connected network）

FNN 前馈神经网络(FeedforwardNeural Network)

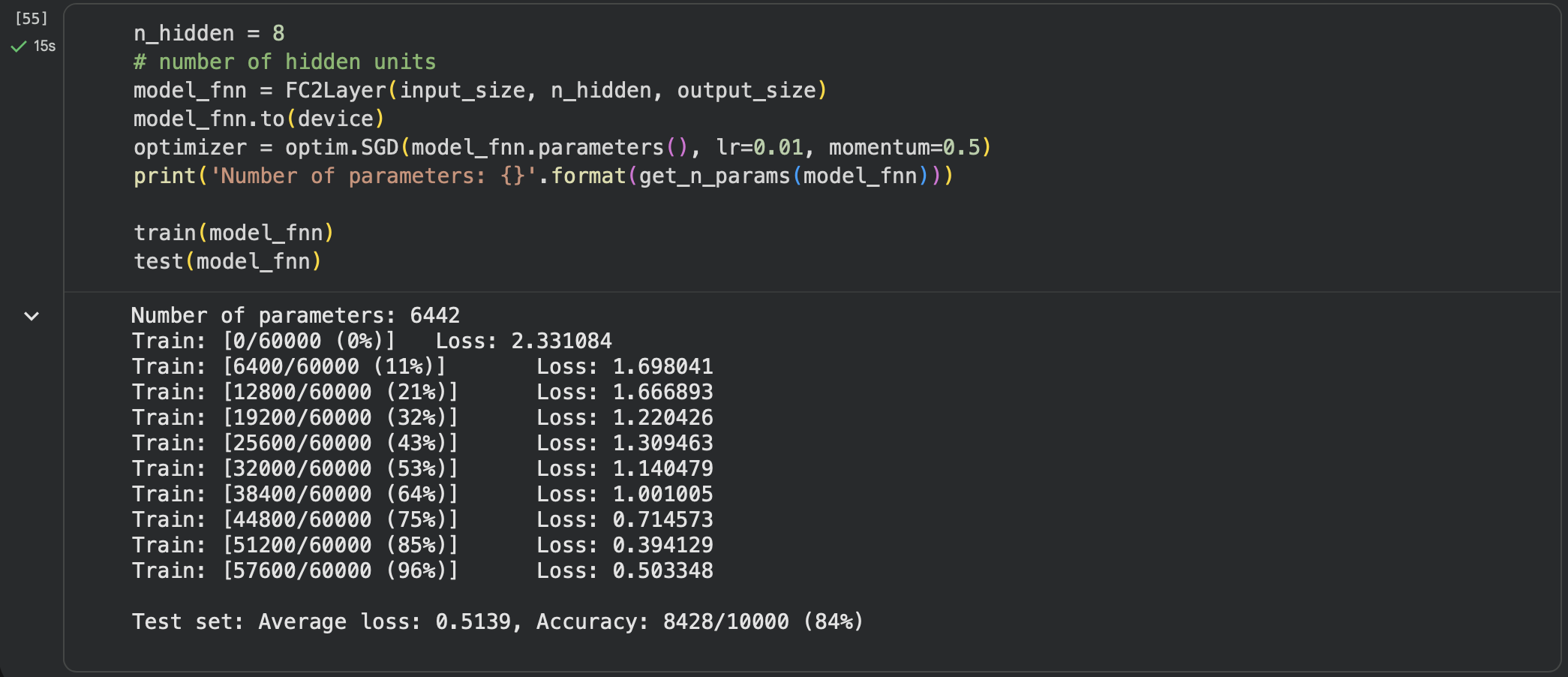
Code4

第四步：在卷积神经网络上训练

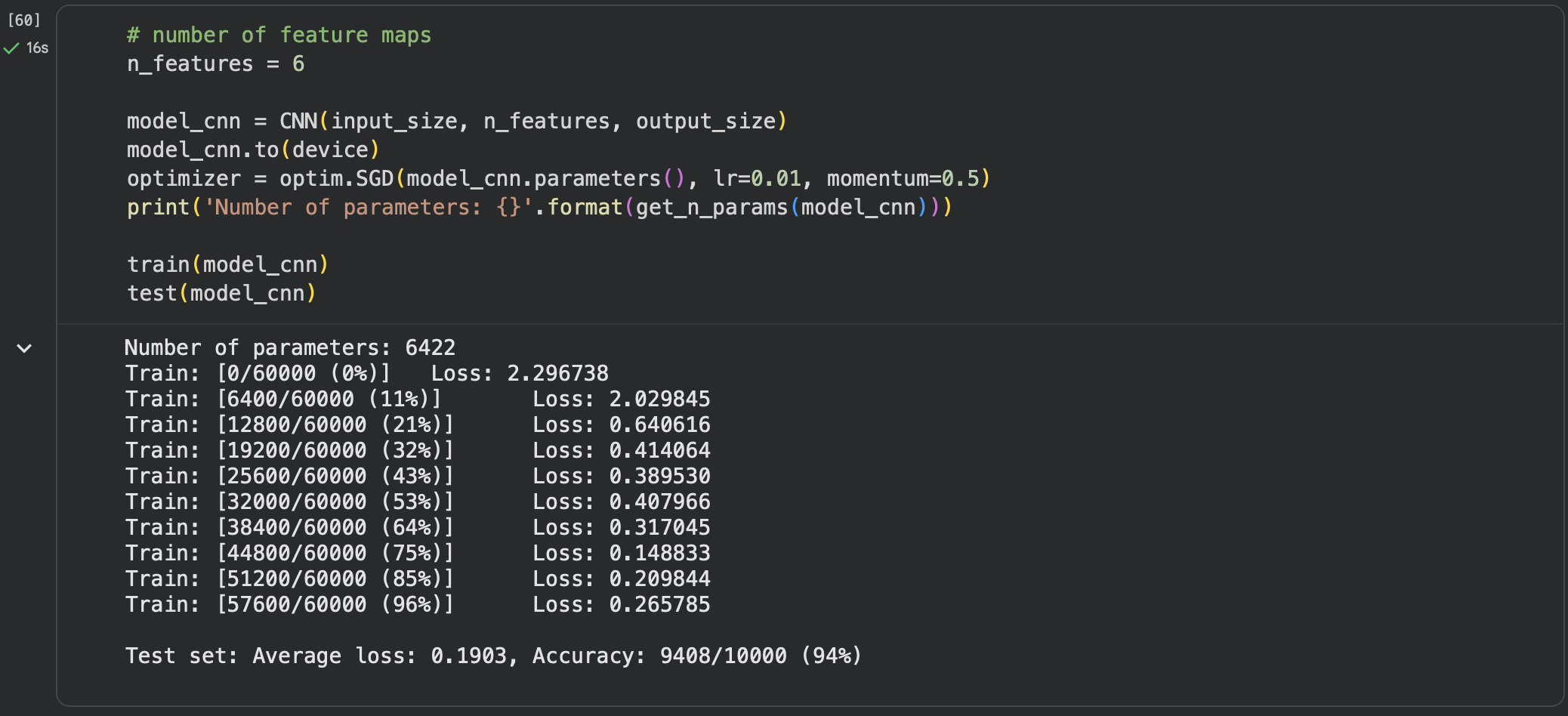
Code5

第五步：打乱像素顺序再次在两个网络上训练与测试

考虑到CNN在卷积与池化上的优良特性，如果我们把图像中的像素打乱顺序，这样卷积和池化就难以发挥作用了，为了验证这个想法，我们把图像中的像素打乱顺序再试试。

首先下面代码展示随机打乱像素顺序后，图像的形态：

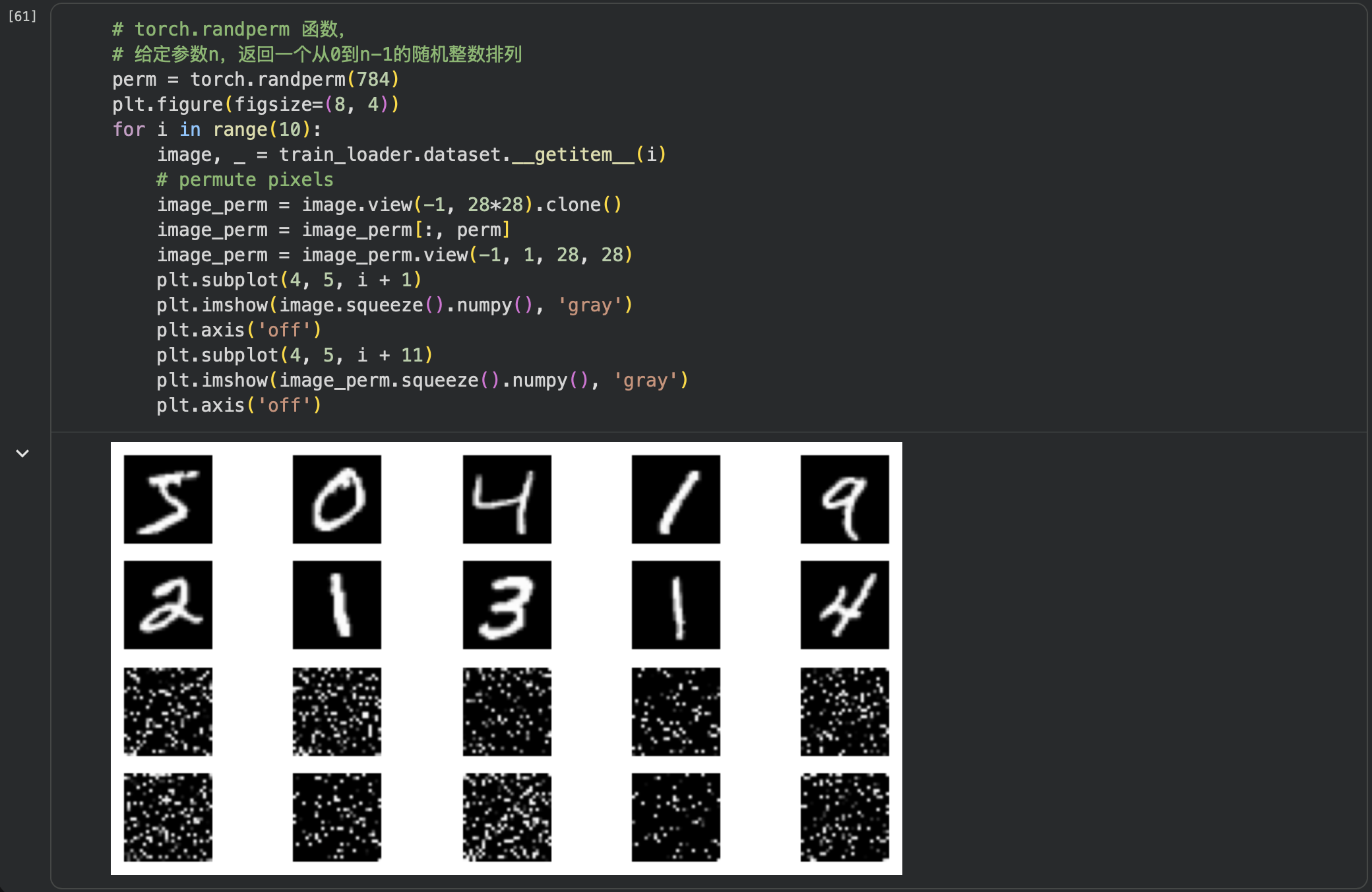
Code6

重新定义训练与测试函数，我们写了两个函数 train_perm 和 test_perm，分别对应着加入像素打乱顺序的训练函数与测试函数。

与之前的训练与测试函数基本上完全相同，只是对 data 加入了打乱顺序操作。

# 对每个 batch 里的数据，打乱像素顺序的函数
def perm_pixel(data, perm):
    # 转化为二维矩阵
    data_new = data.view(-1, 28*28)
    # 打乱像素顺序
    data_new = data_new[:, perm]
    # 恢复为原来4维的 tensor
    data_new = data_new.view(-1, 1, 28, 28)
    return data_new

# 训练函数
def train_perm(model, perm):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        # 像素打乱顺序
        data = perm_pixel(data, perm)

        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % 100 == 0:
            print('Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))

# 测试函数
def test_perm(model, perm):
    model.eval()
    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)

        # 像素打乱顺序
        data = perm_pixel(data, perm)

        output = model(data)
        test_loss += F.nll_loss(output, target, reduction='sum').item()
        pred = output.data.max(1, keepdim=True)[1]                                            
        correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()

    test_loss /= len(test_loader.dataset)
    accuracy = 100. * correct / len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        accuracy))

在全连接网络上训练与测试：

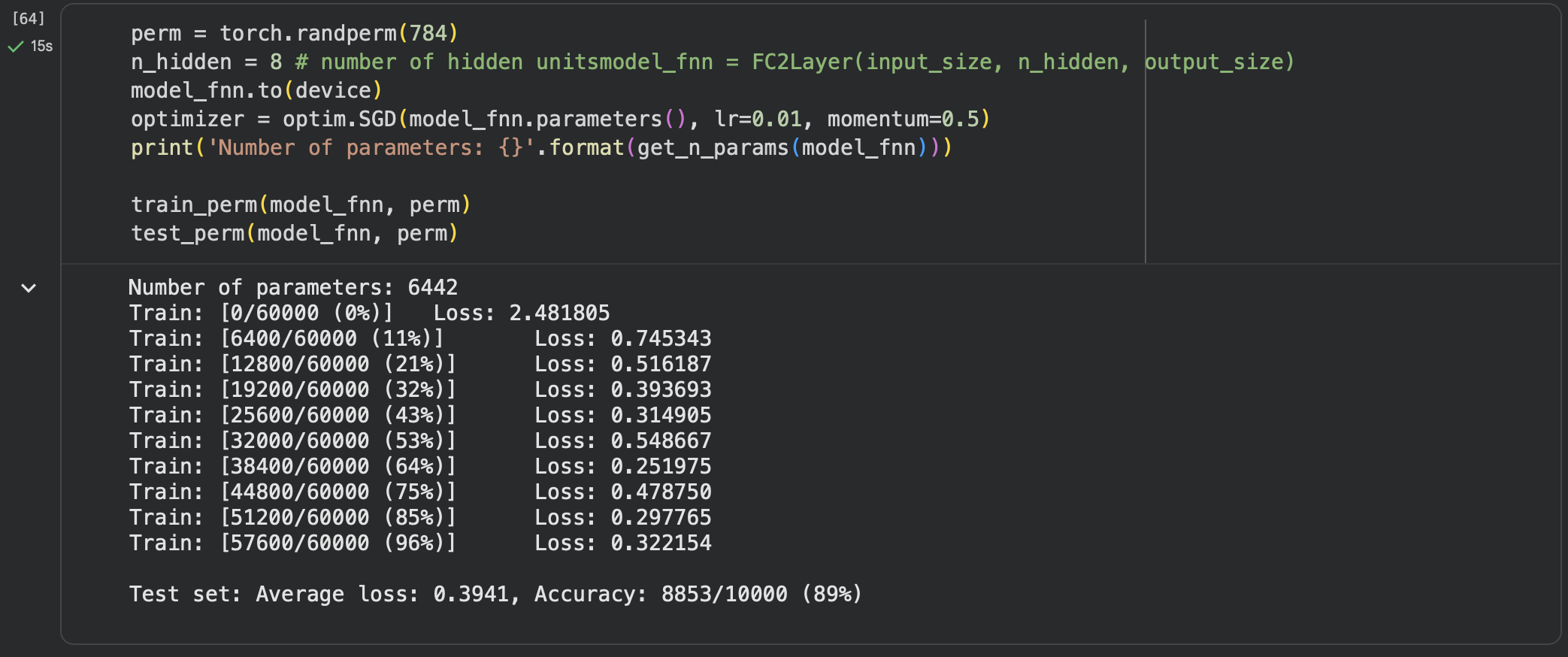
Code7

在卷积神经网络上训练与测试：

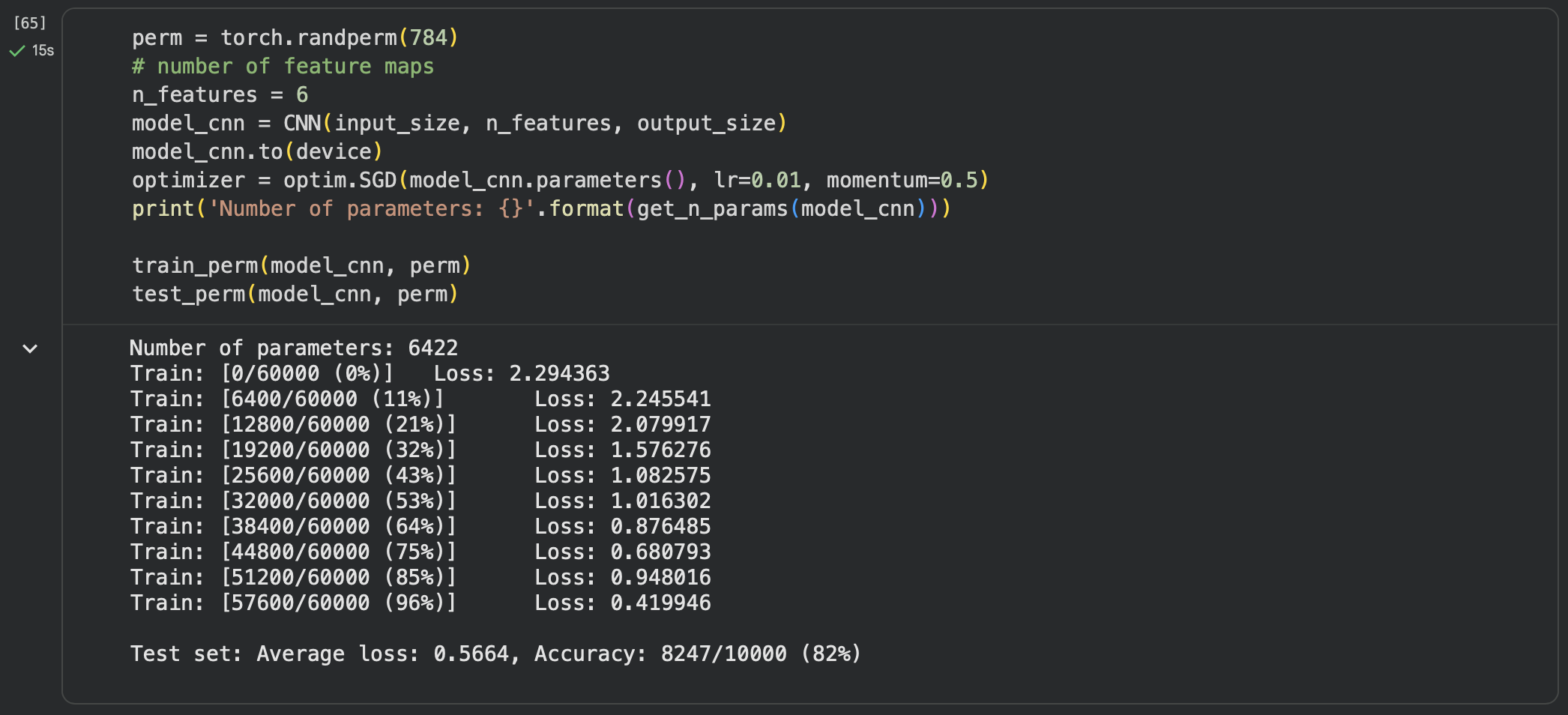
Code8

从打乱像素顺序的实验结果来看，全连接网络的性能基本上没有发生变化，但是卷积神经网络的性能明显下降。

这是因为对于卷积神经网络，会利用像素的局部关系，但是打乱顺序以后，这些像素间的关系将无法得到利用。

分析：以“一定规律”将图片像素打散的方式测试的可行性在于，对每一张图进行了相同的“不规则改动”，这一改动对于图片内容来说是毁灭性的，但是对于FNN来说，被展平(Flatten)的训练集本身的特征只是进行了排序上的改动，规律并没有被打乱，而对于CNN来说，由于像素顺序的打乱，使得图片本身“看起来的”信息丢失，卷积及池化过程中完全无法获得任何有用的信息，相较于FNN反倒效果变得一般。

实验3：使用VGG对CIFAR10分类

VGG是由Simonyan 和Zisserman在文献《Very Deep Convolutional Networks for Large Scale Image Recognition》中提出卷积神经网络模型，其名称来源于作者所在的牛津大学视觉几何组(Visual Geometry Group)的缩写。该模型参加2014年的 ImageNet图像分类与定位挑战赛，取得了优异成绩：在分类任务上排名第二，在定位任务上排名第一。

CIFAR10（Canadian Institute for Advanced Research）是深度学习领域最经典的图像分类基准数据集之一，由 Alex Krizhevsky、Vinod Nair 和 Geoffrey Hinton 整理发布，尤其适合入门级计算机视觉算法的训练与测试。CIFAR10 包含 60000 张 32×32 像素的彩色 RGB 图像，分为 50000 张训练集 + 10000 张测试集，图像分辨率较低，计算成本小，适合快速迭代模型。

Epoch 1: 100%|██████████| 391/391 [00:20<00:00, 18.95it/s, Loss=1.42, Acc=47.5]

Test set: Average loss: 1.1123, Accuracy: 6026/10000 (60.26%)

保存最佳模型，准确率: 60.26%
Epoch 2: 100%|██████████| 391/391 [00:19<00:00, 20.53it/s, Loss=0.94, Acc=66.8]

Test set: Average loss: 0.8780, Accuracy: 7031/10000 (70.31%)

保存最佳模型，准确率: 70.31%
Epoch 3: 100%|██████████| 391/391 [00:19<00:00, 20.24it/s, Loss=0.767, Acc=73.1]

Test set: Average loss: 0.7769, Accuracy: 7356/10000 (73.56%)

保存最佳模型，准确率: 73.56%
Epoch 4: 100%|██████████| 391/391 [00:19<00:00, 20.42it/s, Loss=0.662, Acc=77]

Test set: Average loss: 0.6401, Accuracy: 7754/10000 (77.54%)

保存最佳模型，准确率: 77.54%
Epoch 5: 100%|██████████| 391/391 [00:18<00:00, 20.90it/s, Loss=0.586, Acc=79.6]

Test set: Average loss: 0.6776, Accuracy: 7817/10000 (78.17%)

保存最佳模型，准确率: 78.17%
Epoch 6: 100%|██████████| 391/391 [00:19<00:00, 20.45it/s, Loss=0.533, Acc=81.5]

Test set: Average loss: 0.5979, Accuracy: 7910/10000 (79.10%)

保存最佳模型，准确率: 79.10%
Epoch 7: 100%|██████████| 391/391 [00:19<00:00, 20.21it/s, Loss=0.489, Acc=83.1]

Test set: Average loss: 0.5611, Accuracy: 8128/10000 (81.28%)

保存最佳模型，准确率: 81.28%
Epoch 8: 100%|██████████| 391/391 [00:18<00:00, 21.05it/s, Loss=0.457, Acc=84.3]

Test set: Average loss: 0.5402, Accuracy: 8126/10000 (81.26%)

Epoch 9: 100%|██████████| 391/391 [00:18<00:00, 20.72it/s, Loss=0.417, Acc=85.6]

Test set: Average loss: 0.5032, Accuracy: 8280/10000 (82.80%)

保存最佳模型，准确率: 82.80%
Epoch 10: 100%|██████████| 391/391 [00:19<00:00, 19.86it/s, Loss=0.392, Acc=86.4]

Test set: Average loss: 0.4554, Accuracy: 8469/10000 (84.69%)

保存最佳模型，准确率: 84.69%

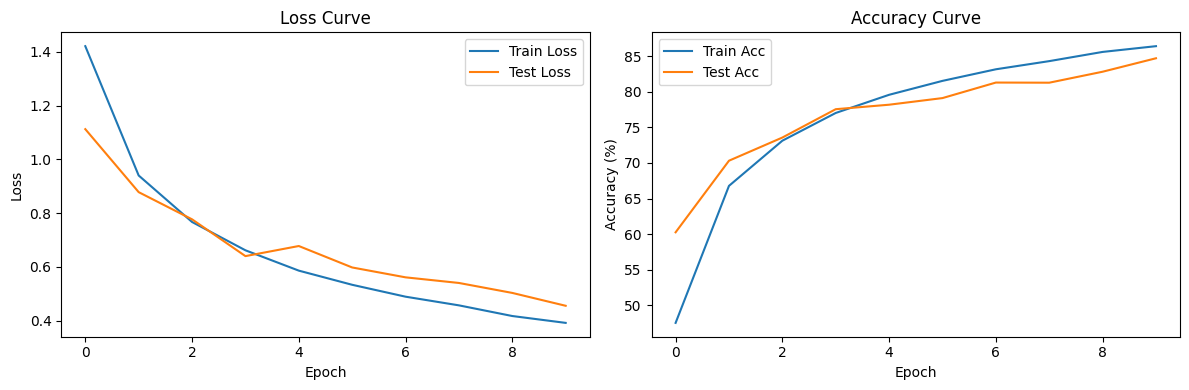
最佳测试准确率: 84.69%

Test set: Average loss: 0.4554, Accuracy: 8469/10000 (84.69%)

加载最佳模型后最终测试准确率: 84.69%

Accuracy of plane : 81.60%
Accuracy of car : 94.10%
Accuracy of bird : 84.20%
Accuracy of cat : 75.60%
Accuracy of deer : 88.10%
Accuracy of dog : 69.50%
Accuracy of frog : 86.50%
Accuracy of horse : 86.60%
Accuracy of ship : 90.80%
Accuracy of truck : 89.90%

实验4：使用ResNet18对CIFAR10分类

ResNet 是如何“保证不退化”的？——不是靠降低学习率，而是结构设计

在学习 ResNet 时，一个非常自然、但又容易被误解的问题是：

如果某一层在当前训练中并没有学到更好的表示，
网络是如何“不退化”、甚至还能继续加深的？
是不是通过降低学习率，牺牲更新幅度来换稳定性？

答案是：不是。

ResNet 的“不退化”并不依赖训练技巧，而是来自网络结构本身。

1. 一个关键误区：不是“保留上一轮训练结果”

很多人（包括我一开始）会下意识地这样理解：

如果这一轮训练没学好，ResNet 会“保留上一次的 shortcut”

但这是不准确的。

ResNet 不涉及时间维度上的“上一轮 / 上一次”，它做的是：

在同一次 forward 中，始终保留当前输入 x 本身。

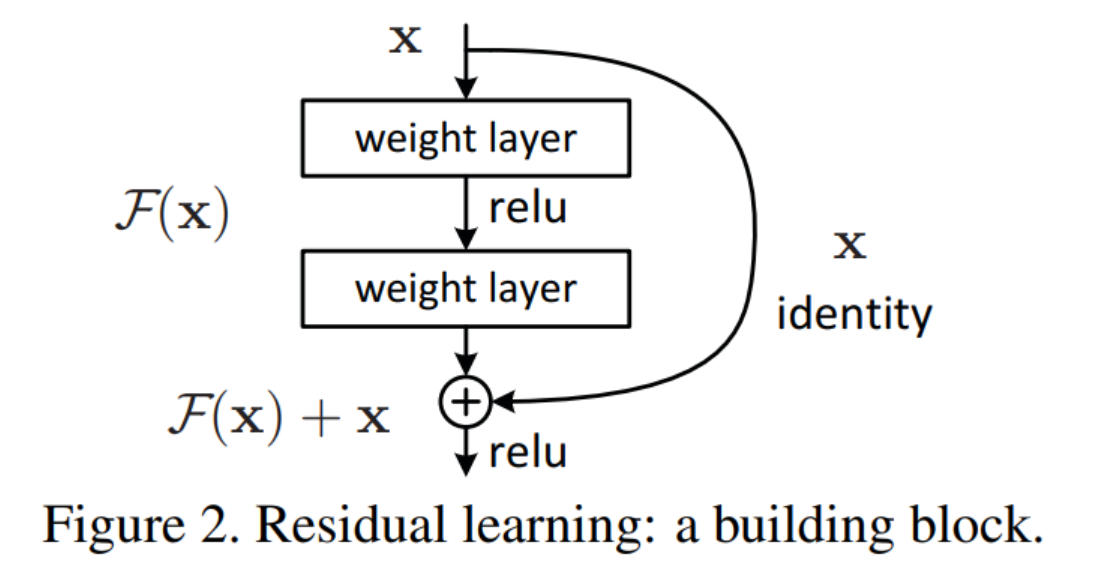
2. ResNet 的核心公式

在残差块中，输出不是直接：

\[H(x) = F(x)\]

而是：

\[H(x) = F(x) + x\]

其中：

$x$：当前残差块的输入
$F(x)$：由若干卷积层学习到的“残差”

shortcut 并不是训练得到的，而是写死在网络结构里的。

3. “不退化”是如何实现的？

3.1 如果这一层什么都没学会

假设由于初始化、梯度或数据原因，这一层的卷积几乎没起作用：

\[F(x) \approx 0\]

那么输出就是：

\[H(x) \approx x\]

也就是说：

这一层在功能上等价于“恒等映射”

网络变深了，但行为几乎没变。

3.2 对比普通深层网络

普通深层 CNN 中：

\[H(x) = W_2 \sigma(W_1 x)\]

如果某一层学不好：

权重扰乱表示
非线性破坏信息

输出一定会变差，深度反而成为负担。

4. shortcut 的“保底机制”是结构性的

ResNet 的逻辑可以总结为一句话：

“你不管学成什么样，我都把原始输入 x 原样加回来。”

这不是：

early stopping
保存最优权重
回滚模型参数

而是前向传播中就已经完成的设计。

5. 从梯度角度看：为什么深层也能训练？

对残差结构求导：

\[H(x) = F(x) + x\] \[\frac{\partial H}{\partial x} = \frac{\partial F}{\partial x} + 1\]

这个 +1 极其关键：

即使 $\frac{\partial F}{\partial x} \to 0$
梯度依然可以通过 shortcut 直接传播

这从根本上缓解了深层网络中的梯度消失问题。

6. 那学习率会不会“变低”？

不会。

ResNet 不会自动修改学习率
学习率调度（Step / Cosine / Warmup）与是否使用残差是正交的

同样的 optimizer 和 learning rate：

普通深层 CNN：可能退化或无法收敛
ResNet：可以稳定训练

7. 真正的“代价”是什么？

虽然 ResNet 不靠降低学习率，但它确实付出了一种代价：

每一层对最终输出的“影响力被削弱了”。

原因在于：

参数只存在于 $F(x)$
输出始终是 $x + F(x)$

因此：

参数更新对输出的影响是“修正项”
而不是“完全重写表示”

8. 这是一种“克制而稳定”的学习方式

可以这样理解：

普通网络：

每一层都试图“决定一切”
ResNet：

每一层只负责“微调现有表示”

这使得网络：

单层更保守
但可以安全地堆叠到非常深

9. 这不是“牺牲速度换稳定”

更准确地说是：

没有 ResNet，深层网络根本学不了；
有了 ResNet，才谈得上速度和表达能力。

这也是为什么后续模型
（Pre-Activation ResNet、DenseNet、Transformer）
几乎全部保留了 residual 结构。

10. 总结

ResNet 的“不退化”不是靠降低学习率
而是通过
$H(x) = x + F(x)$ 的结构设计
shortcut 提供了恒等映射与梯度直通路径
代价是单层更新更“克制”
收益是网络可以无限加深而不崩

ResNet 的本质不是让每一层都变强，
而是允许每一层在“学不好时，选择什么都不做”。

思考问题：

dataloader 里面 shuffle 取不同值有什么区别？ transform 里，取了不同值，这个有什么区别？ epoch 和 batch 的区别？ 1x1的卷积和 FC 有什么区别？主要起什么作⽤？

1. DataLoader 里的 `shuffle` 参数

作用：shuffle=True在每个 epoch 开始时打乱数据顺序。避免模型记住数据顺序，增强泛化能力。

2. Transform 里取不同值

作用：用于数据预处理和增强（data augmentation）。
不同值的影响：
- 对训练集：
  - 可以随机裁剪、旋转、翻转、加噪声等 → 增强数据多样性 → 减少过拟合。
- 对测试集：
  - 通常使用固定的 transform（如 Resize + ToTensor + Normalize） → 保证评估一致性。

3. Epoch 和 Batch 的区别

Epoch（轮次）全部训练集数据被模型完整训练一次，称为一个 epoch。
Batch（批次）一次送入网络训练的数据量。

4. 1x1 卷积 vs 全连接（FC）

经过1x1 卷积后的数据仍然拥有空间二维结构，而经过全连接(FC)的数据是被展平的，没有了空间信息
1x1 卷积常用于实现压缩深度/维度/通道数(Depth/Channel)

一些思考：既然可以通过打散像素的方式，让（图片）数据的信息不能被CNN较为良好地发现和处理，那么是否可以找到打散像素这一过程的逆过程，使得经过此过程，在后续的卷积以及池化过程中，不直观明显的信息得以展示？仔细再想一下，这一番过程似乎同样是一种特殊的“卷积”，但是不同于传统矩形的卷积核，如果用卷积核的方式实现这一过程是否会造成效率的降低？在此之前，值得考虑的是，实际情况中是否真的存在这样的被特定方式打散的图片数据？而除了图片之外，其他模态的数据信息是否有这样的特性？总而言之，疑惑点在于，现在认识到的各类卷积核都是矩形的，且相对较小，重要的特征是否都能被找到？

###

Share on

X Facebook LinkedIn Bluesky

Jackthin Shin

25秋深度学习训练营-第2周：卷积神经网络

第2周：卷积神经网络

代码练习

实验1: 使用 LeNet 对 MNIST 数据集分类

实验2：MNIST数据集分类(使用参数接近的MLP和CNN分别对MNIST数据集分类)

第一步：加载数据（MNIST）

第二步：创建网络

第三步：在小型全连接网络上训练（Fully-connected network）

第四步：在卷积神经网络上训练

第五步：打乱像素顺序再次在两个网络上训练与测试

实验3：使用VGG对CIFAR10分类

实验4：使用ResNet18对CIFAR10分类

ResNet 是如何“保证不退化”的？——不是靠降低学习率，而是结构设计

1. 一个关键误区：不是“保留上一轮训练结果”

2. ResNet 的核心公式

3. “不退化”是如何实现的？

3.1 如果这一层什么都没学会

3.2 对比普通深层网络

4. shortcut 的“保底机制”是结构性的

5. 从梯度角度看：为什么深层也能训练？

6. 那学习率会不会“变低”？

7. 真正的“代价”是什么？

8. 这是一种“克制而稳定”的学习方式

9. 这不是“牺牲速度换稳定”

10. 总结

思考问题：

1. DataLoader 里的 `shuffle` 参数

2. Transform 里取不同值

3. Epoch 和 Batch 的区别

4. 1x1 卷积 vs 全连接（FC）

Share on

You May Also Enjoy

25秋深度学习训练营-第1周：深度学习基础

Quote

计导试验报告6

Jackthin Shin

第2周：卷积神经网络

代码练习

实验1: 使用 LeNet 对 MNIST 数据集分类

实验2：MNIST数据集分类(使用参数接近的MLP和CNN分别对MNIST数据集分类)

第一步： 加载数据 （MNIST）

第二步：创建网络

第三步：在小型全连接网络上训练（Fully-connected network）

第四步：在卷积神经网络上训练

第五步：打乱像素顺序再次在两个网络上训练与测试

实验3：使用VGG对CIFAR10分类

实验4：使用ResNet18对CIFAR10分类

ResNet 是如何“保证不退化”的？——不是靠降低学习率，而是结构设计

1. 一个关键误区：不是“保留上一轮训练结果”

2. ResNet 的核心公式

3. “不退化”是如何实现的？

3.1 如果这一层什么都没学会

3.2 对比普通深层网络

4. shortcut 的“保底机制”是结构性的

5. 从梯度角度看：为什么深层也能训练？

6. 那学习率会不会“变低”？

7. 真正的“代价”是什么？

8. 这是一种“克制而稳定”的学习方式

9. 这不是“牺牲速度换稳定”

10. 总结

思考问题：

1. DataLoader 里的 shuffle 参数

2. Transform 里取不同值

3. Epoch 和 Batch 的区别

4. 1x1 卷积 vs 全连接（FC）

Share on

You May Also Enjoy

25秋深度学习训练营-第1周：深度学习基础

Quote

计导试验报告6

第一步：加载数据（MNIST）

1. DataLoader 里的 `shuffle` 参数