Jackthin Shin

I am who I am, I have nothing to hide.

2 minute read

第1周：深度学习基础

学习内容：https://oucai.club/classes/dl/week01#第1周-深度学习基础

学习视频：https://www.jianguoyun.com/p/Dde3HS8QrKKIBhi2xpEGIAA

学习要求：

  • 深度学习的入门知识
  • pytorch 基础练习，螺旋数据分类代码练习

1、视频学习

学习视频：深度学习基础，主要内容包括：

  • 浅层神经⽹络：⽣物神经元到单层感知器，多层感知器，反向传播和梯度消失
  • 神经⽹络到深度学习：逐层预训练，⾃编码器和受限玻尔兹曼机

2、代码练习

可以在Google Colaboratory开发Deep Learning Applications，它自带免费的Tesla K80 GPU。

1. PyTorch 基础练习

什么是 PyTorch ? PyTorch是一个python库，它主要提供了两个高级功能：

  • GPU加速的张量计算
  • 构建在反向自动求导系统上的深度神经网络

1. 定义数据

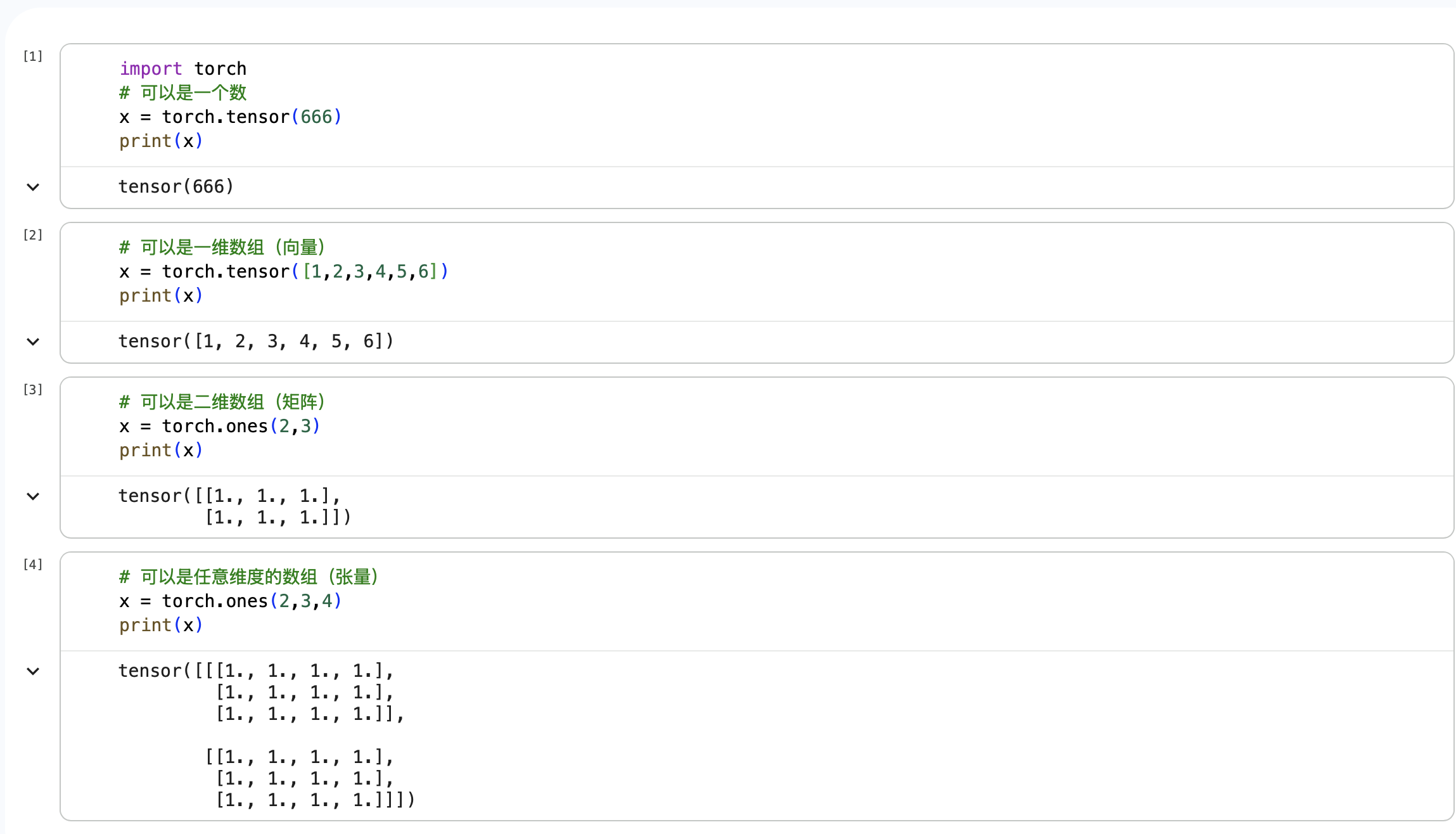
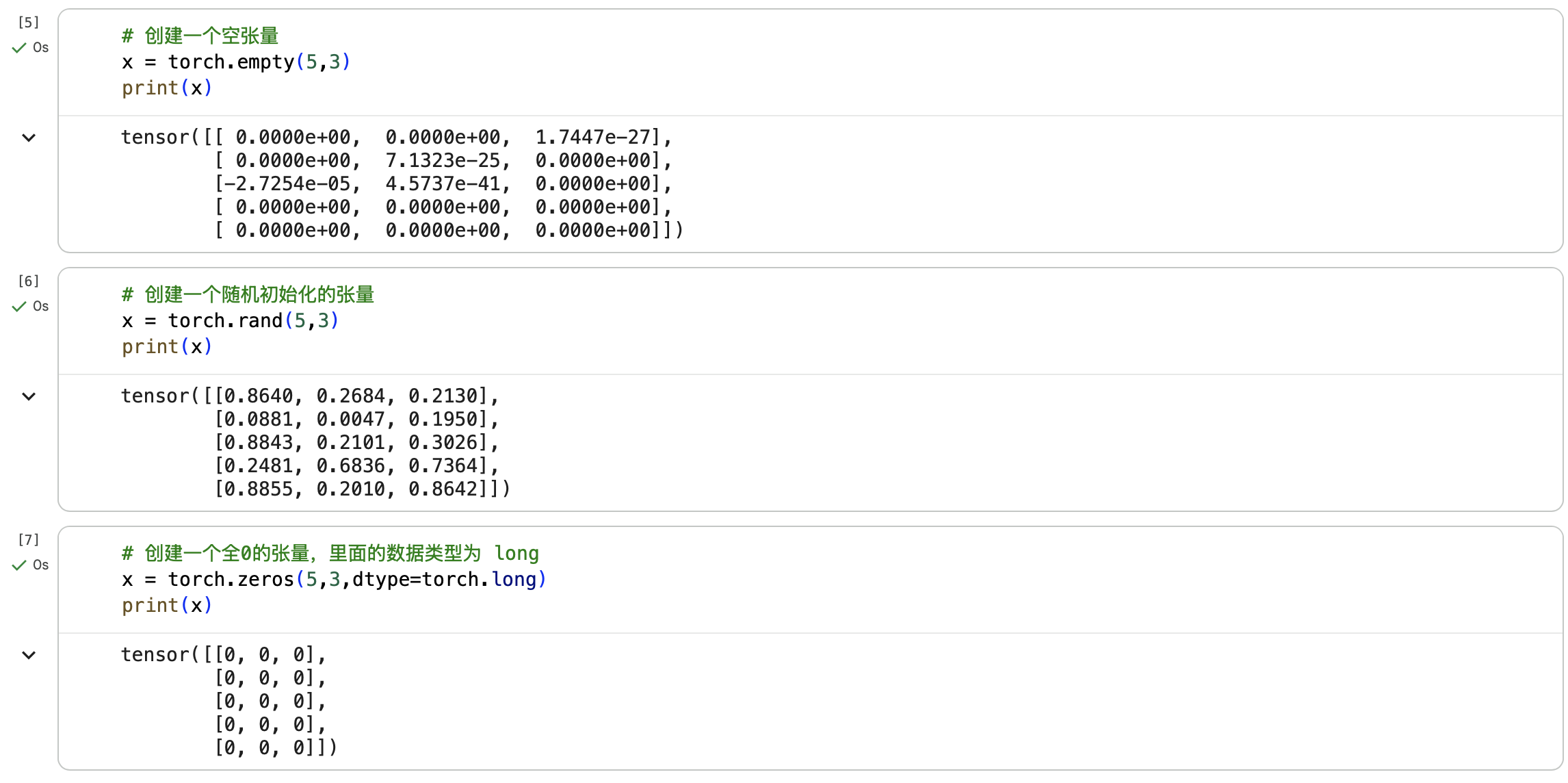
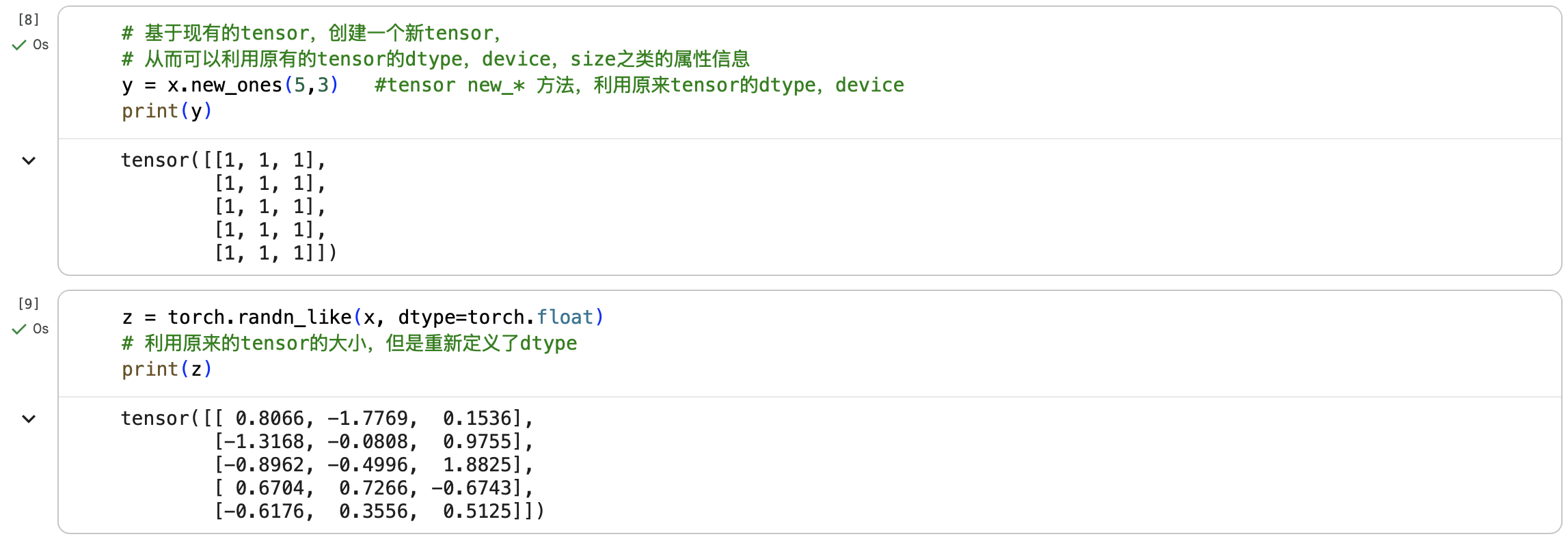
Code1 Code2 Code3

Tensor支持各种各样类型的数据，包括：

torch.float32, torch.float64, torch.float16, torch.uint8, torch.int8, torch.int16, torch.int32, torch.int64

2. 定义操作

凡是用Tensor进行各种运算的，都是Function

最终，还是需要用Tensor来进行计算的，计算无非是

基本运算，加减乘除，求幂求余
布尔运算，大于小于，最大最小
线性运算，矩阵乘法，求模，求行列式
基本运算包括： abs/sqrt/div/exp/fmod/pow ，及一些三角函数 cos/ sin/ asin/ atan2/ cosh，及 ceil/round/floor/trunc 等

布尔运算包括： gt/lt/ge/le/eq/ne，topk, sort, max/min

线性计算包括： trace, diag, mm/bmm，t，dot/cross，inverse，svd 等

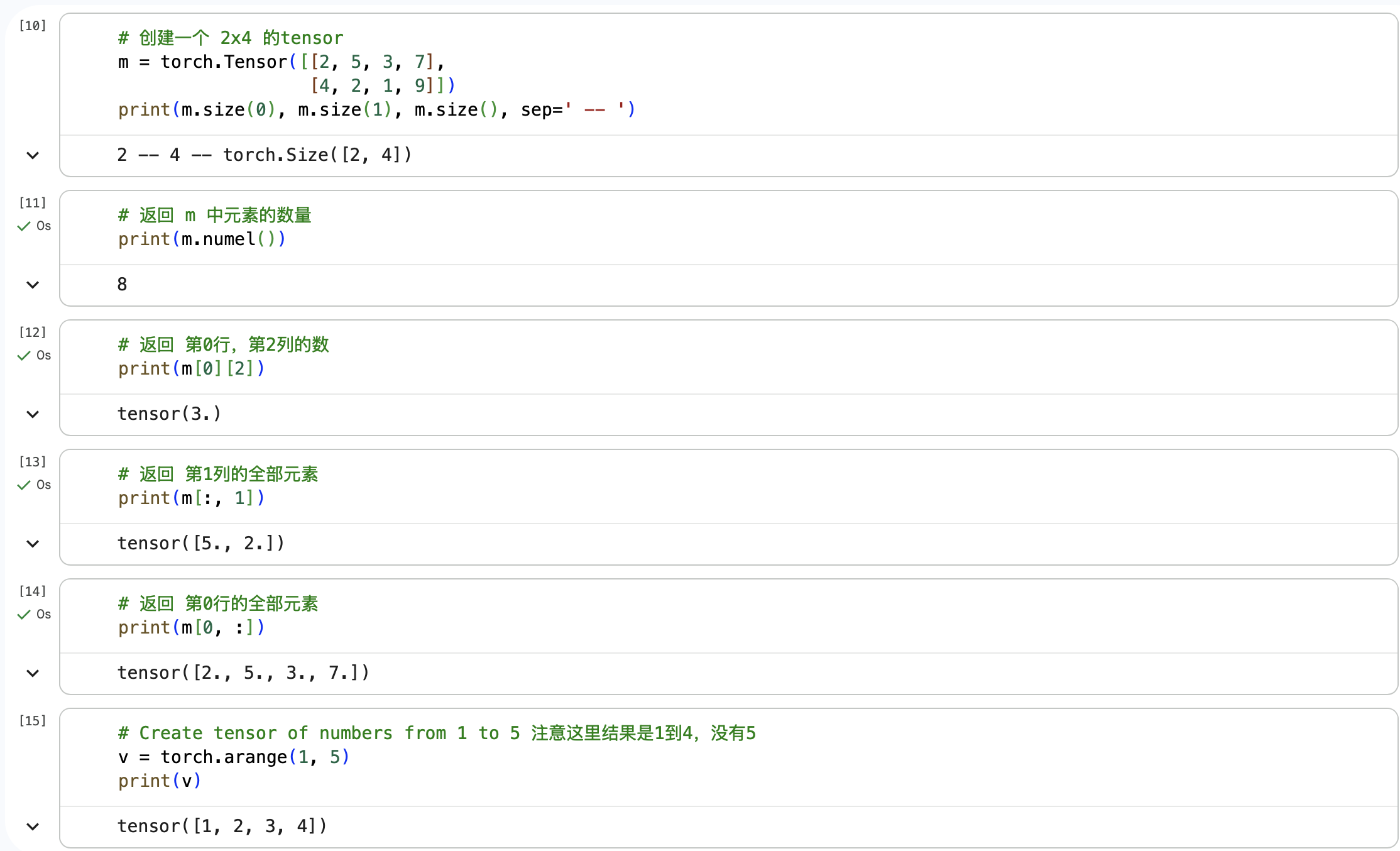
Code4

在对m与v进行矩阵乘法时，报错如下

Error

原因在于在前文代码中，m的dtype为float，而v的dtype为Long

因此，将代码m @ v改为m @ v.float()，把矩阵v的dtype转化为float进行乘法操作

Code5

后续需要进行矩阵乘法的同样要保证两者dtype一致

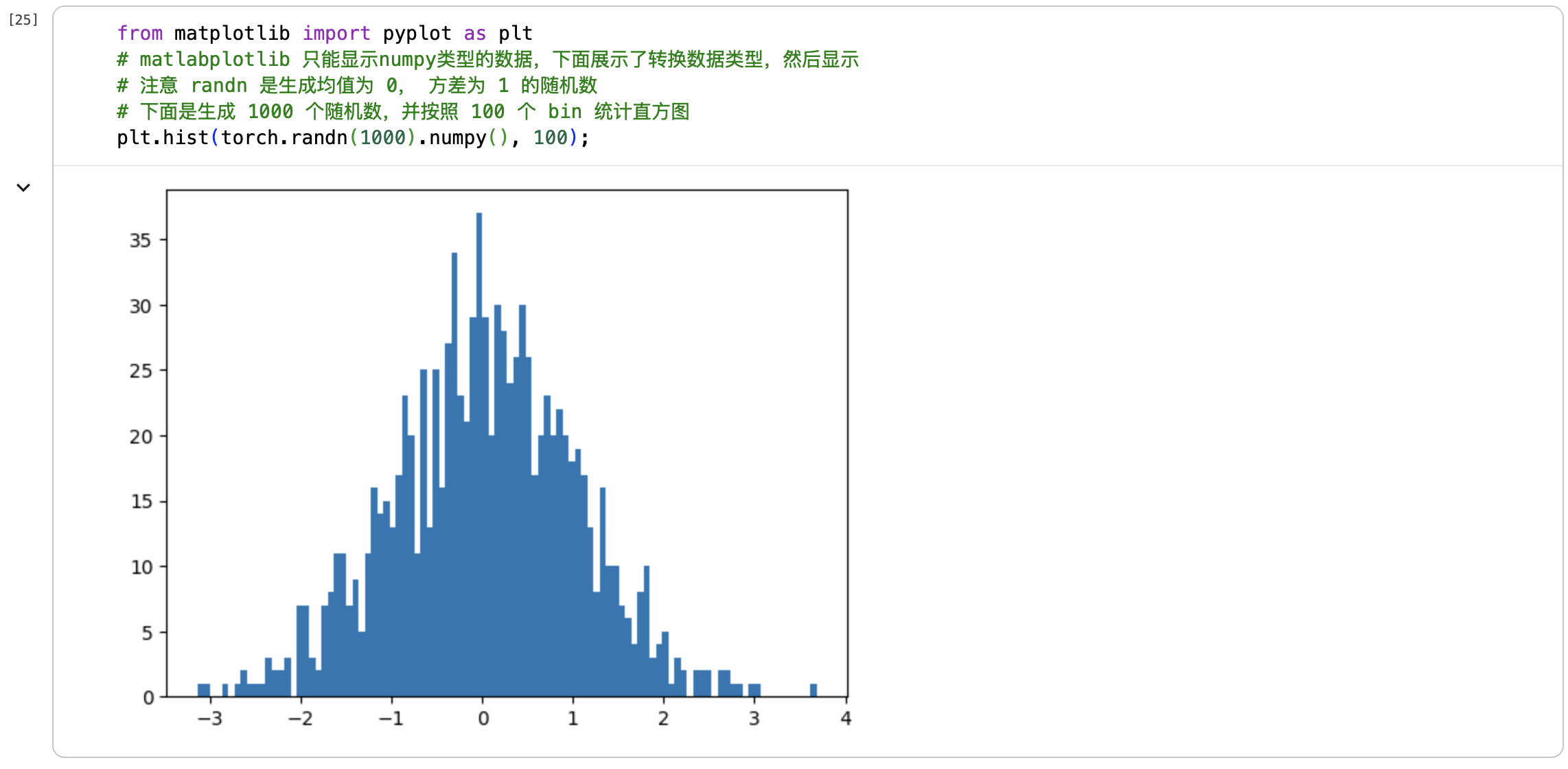
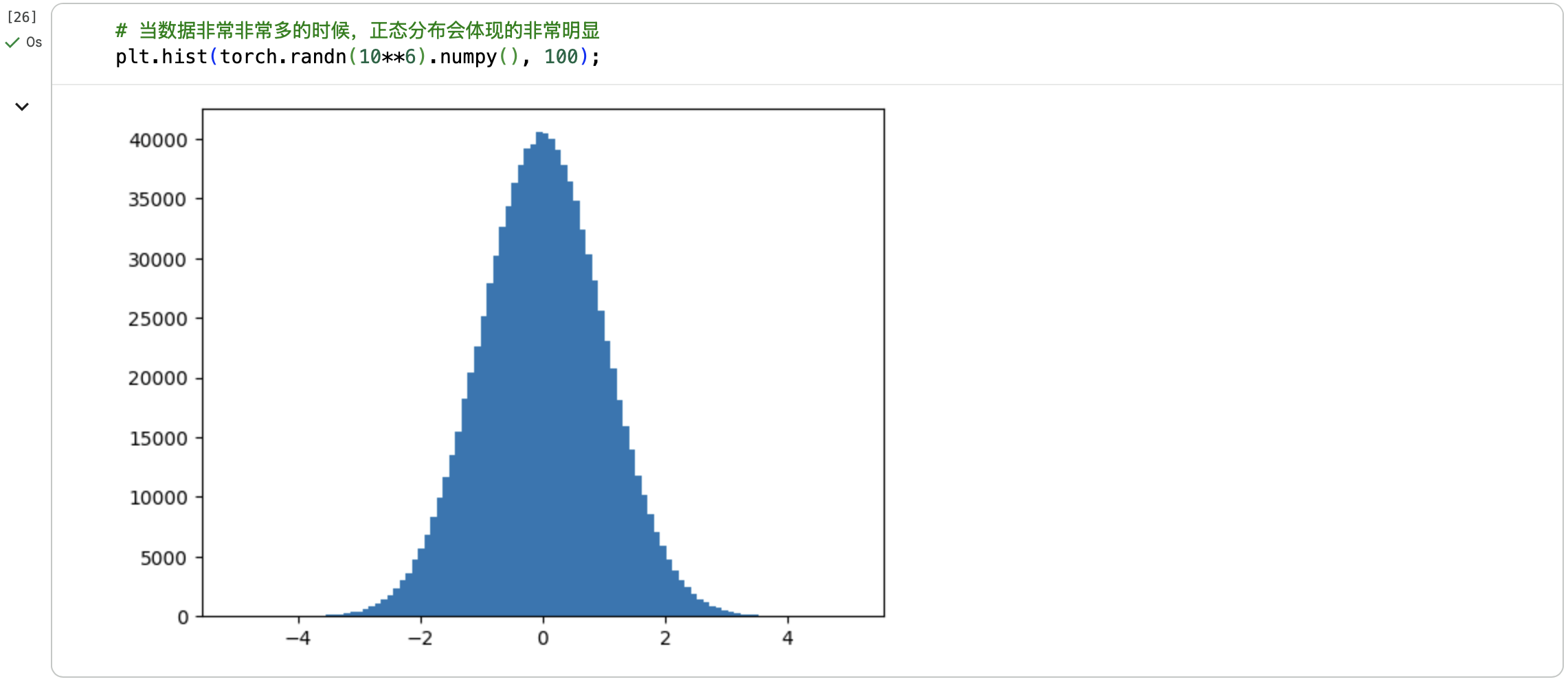
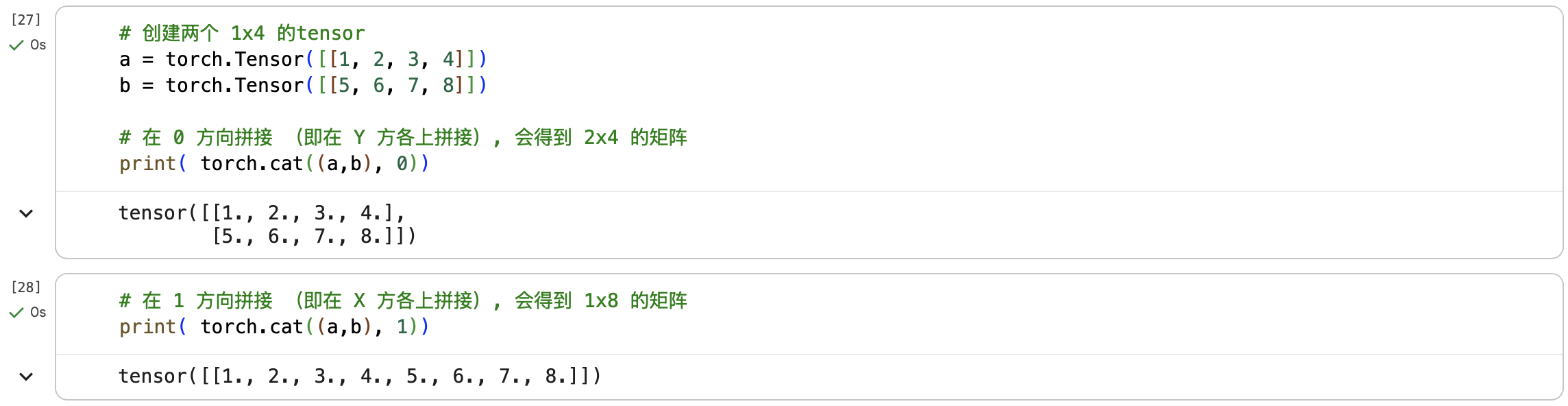
Code6 Code7 Code8 Code9

更多参考PyTorch中文文档

2. 螺旋数据分类

2.1 准备工作

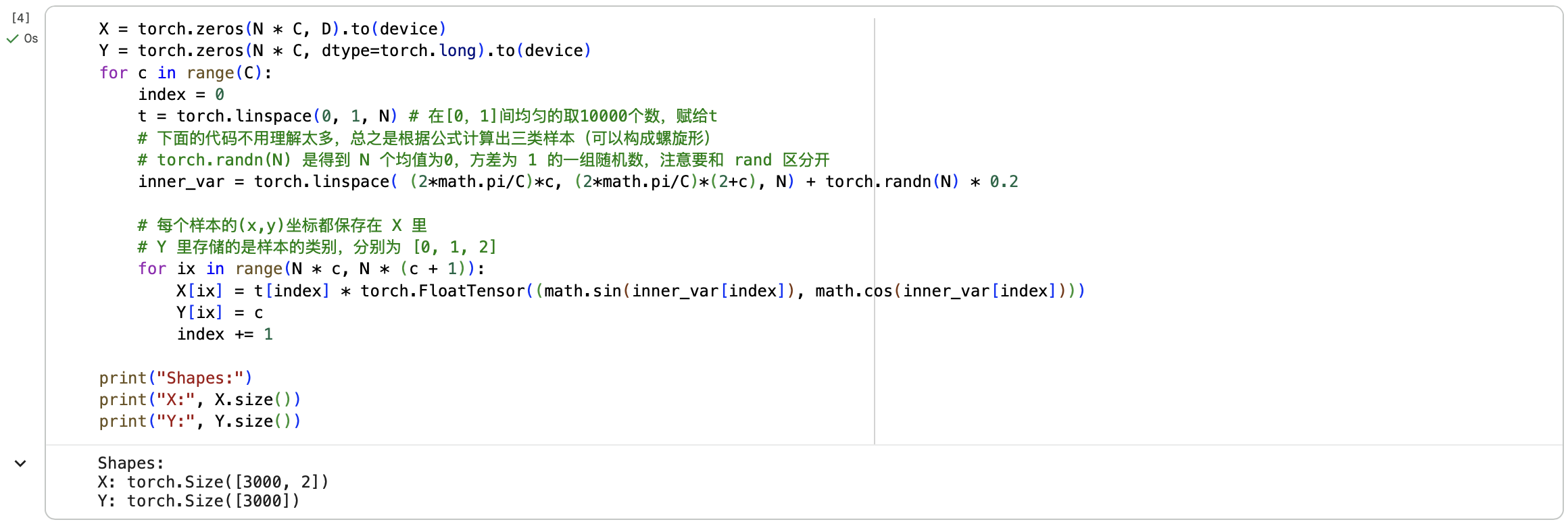
Code10 Code11 Code12

2.2 开始分类

第一步：构建线性模型分类

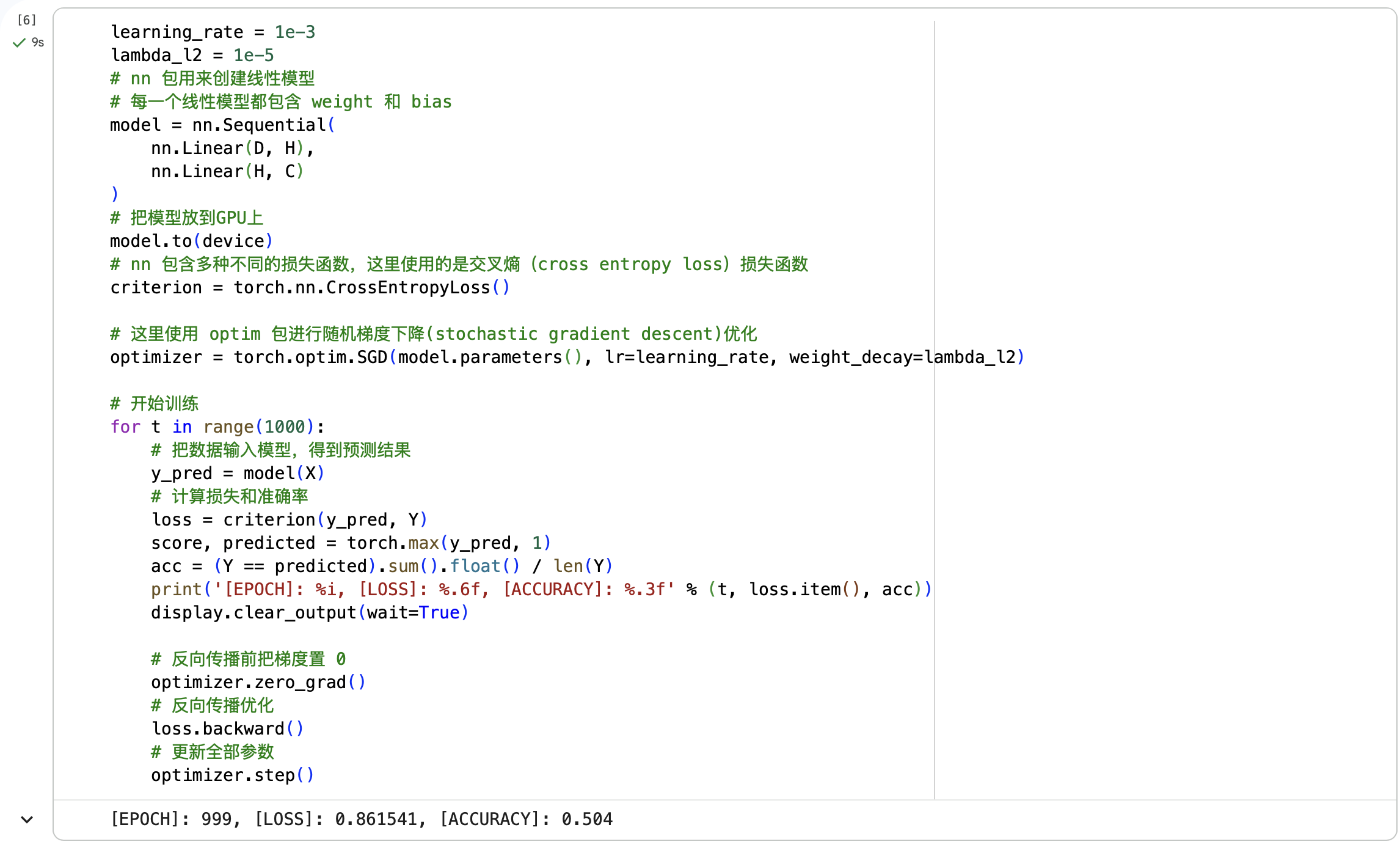
Code13

第二步：输出部分数据的预测结果，并观察

Code14 Code15

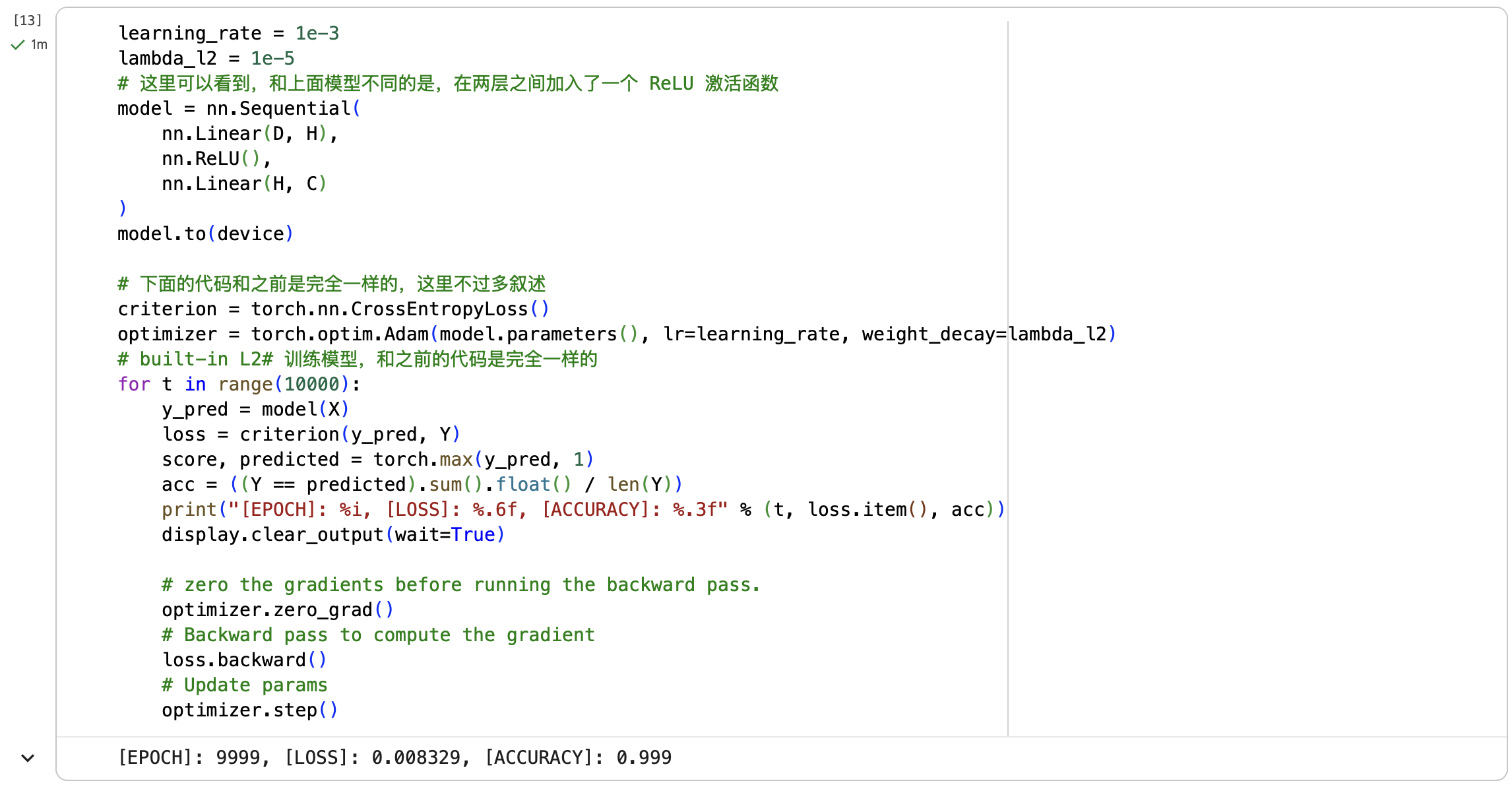
第三步：构建两层神经网络分类

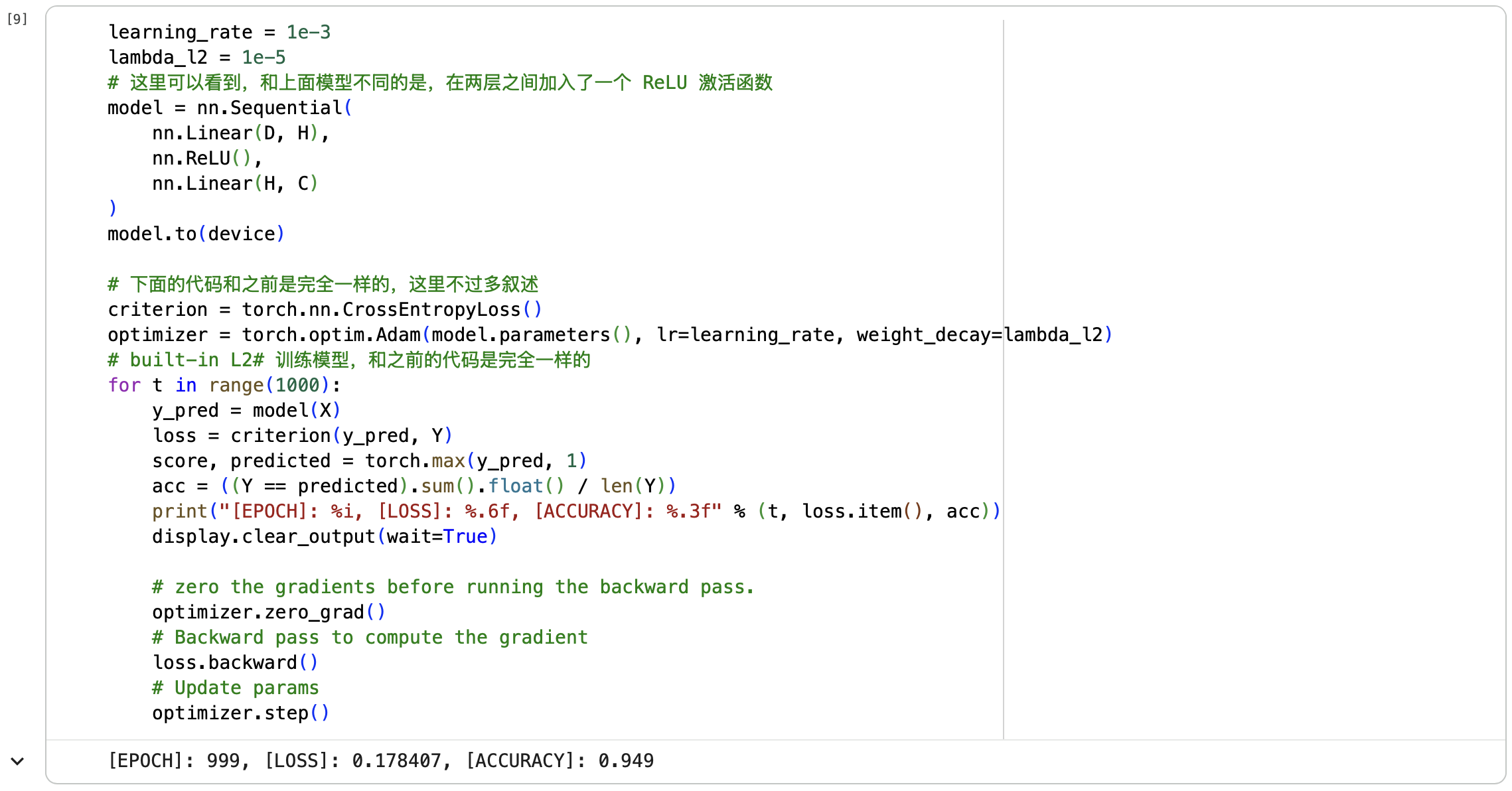
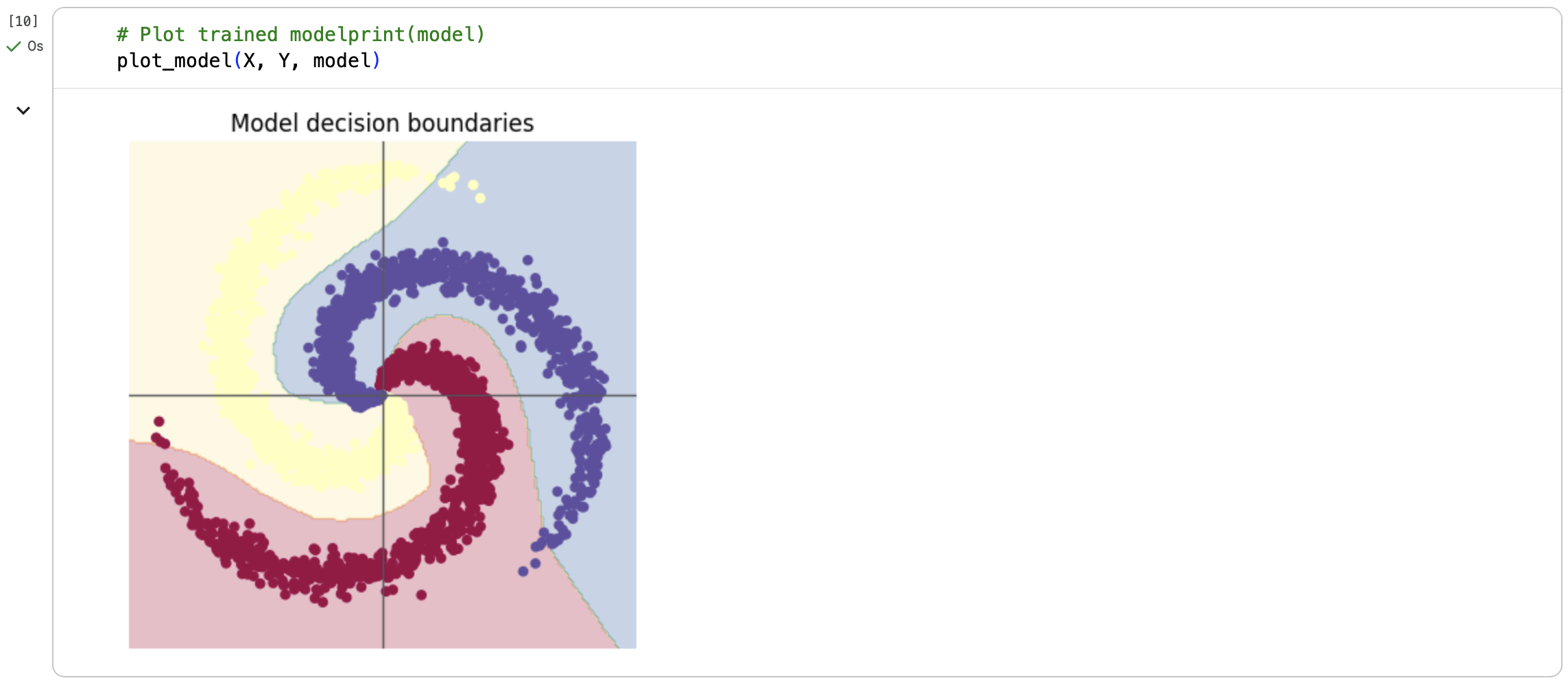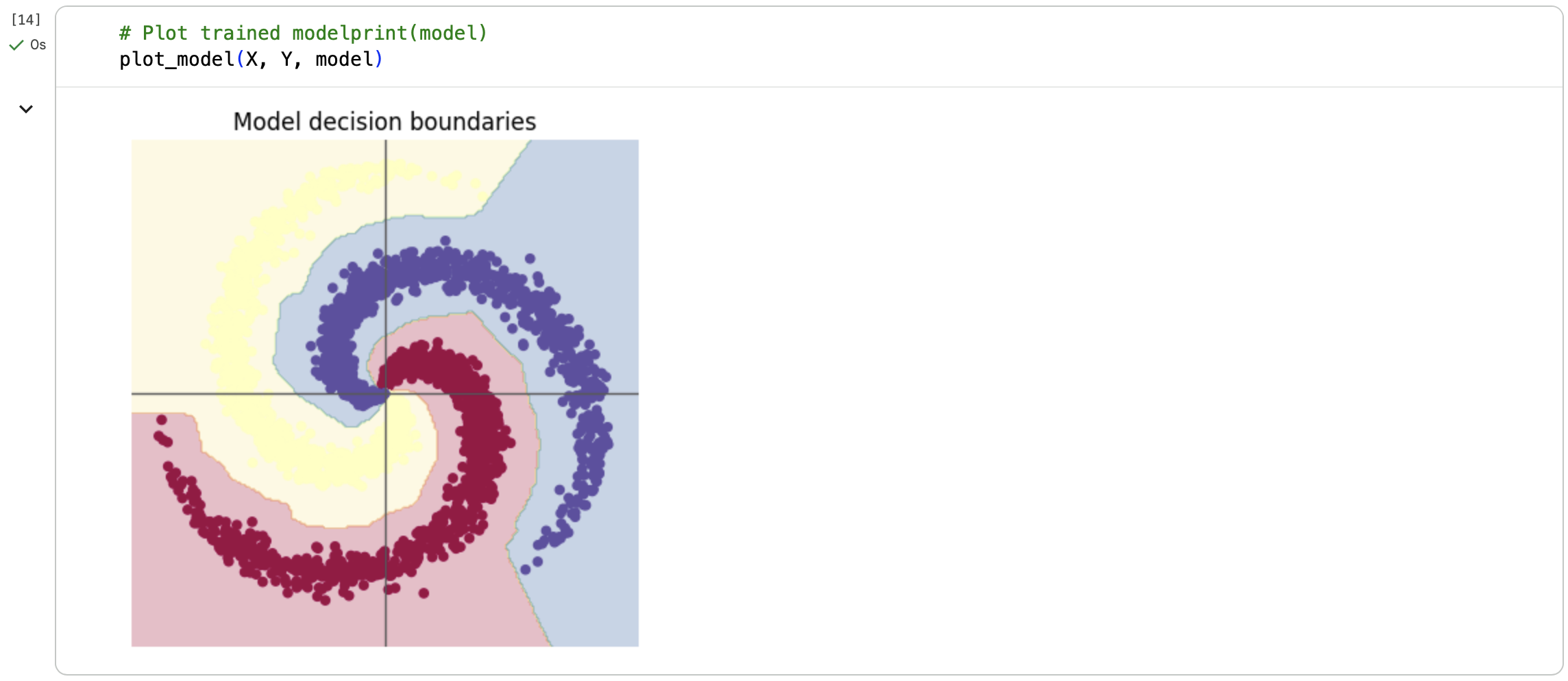
Code16 Code17 若将循环训练次数从1000次改为10000次可以发现：[LOSS]从0.178407变为了0.008329，精度有了不小的提升。观察图片也可以发现分类效果更好。 Code18 Code19

2.3 思考ReLU函数（Rectified Linear Unit）的用处

没有ReLU激活函数时：

\[f(x)=x\]

而有了ReLU激活函数之后：

\[ReLU(x)=max(0,x)\]

在没有激活函数时，多层 Linear 本质仍是线性变换；加入 ReLU 后，引入了非线性，网络可以学习非线性决策边界，表达能力大幅提升。 反映到图像上，未加入激活函数时，图像的分界线为线性（直线）；而在加入ReLU激活函数后，图像的分界线变成了非线性（曲线），更好地实现了螺旋数据的分类。

3、问题总结思考

1、AlexNet有哪些特点？为什么可以比LeNet取得更好的性能？ 2、激活函数有哪些作⽤？ 3、梯度消失现象是什么？ 4、神经网络是更宽好还是更深好？ 5、为什么要使⽤Softmax? 6、SGD 和 Adam 哪个更有效？

1、AlexNet有哪些特点？为什么可以比LeNet取得更好的性能？

相比于LeNet，AlexNet有以下优势：

  • 引入 ReLU 激活函数（首次大规模使用）
    • LeNet 使用的是 sigmoid / tanh，存在梯度消失；
    • ReLU 训练更快、收敛速度快数倍，还能避免梯度消失。
  • 使用 Dropout 防止过拟合
    • 在全连接层中加入 Dropout（p=0.5），减少 co-adaptation。
  • 其他
    • 更深更宽的网络结构
    • 使用局部响应归一化
    • 大规模数据 + 大卷积核 + 大步长
    • ……

2、激活函数有哪些作⽤？

正如思考ReLU函数（Rectified Linear Unit）的用处中提到的：

使用激活函数可以为模型引入非线性，使神经网络具备拟合复杂函数的能力。\(W2​(W1​x)=(W2​W1​)x\)如果没有激活函数，所有层都是线性变换。多层结构等价于一层线性层，无论堆多深都不可能拟合复杂的决策边界。

除此以外，激活函数还可以：

  • 决定梯度流动方式，影响训练稳定性与收敛速度
  • 控制输出范围，帮助优化和数值稳定性
  • ……

Sigmoid / Tanh：饱和区梯度接近 0 → 容易梯度消失

\[\sigma(x)=\frac{1}{1+e^{-x}}\] \[\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\]

ReLU：梯度恒为 1（正区）→ 深层网络易训练

\[\text{ReLU}(x)=\max(0,\,x)\]

Leaky ReLU / GELU：进一步改善 ReLU 的“坏死问题”

\[\text{LeakyReLU}(x)= \begin{cases} x, & x>0 \\ \alpha x, & x\le 0 \end{cases}\] \[\text{GELU}(x)=0.5x\left(1+\tanh\left[\sqrt{\frac{2}{\pi}} \left(x+0.044715x^3\right)\right]\right)\]

3、梯度消失现象是什么？

梯度消失指的是在深度神经网络中，反向传播时梯度在逐层传递过程中变得极其微小，最终接近于 0，导致前面（靠近输入层）的参数几乎无法更新，模型难以训练。

在有导师学习的网络的训练过程中，每一轮训练需要对权重（也就是网络中的连接）进行改动，以减小误差，提高网络拟合程度，而在多隐含层的深度神经网络中，为了调整隐含层中的权重，需要使用误差反传算法，也就是BP（Back Propagation），然而在往回传的过程中，可能因为激活函数的缺陷，进入饱和区，导致梯度接近/等于0，误差无法得到修复，训练停滞。

梯度消失（Vanishing Gradient）公式说明

1. Sigmoid 导数

Sigmoid 函数：

\[\sigma(x) = \frac{1}{1+e^{-x}}\]

对应导数为：

\[\sigma'(x) = \sigma(x)\,(1-\sigma(x)) \approx 0 \quad \text{（当进入饱和区时）}\]
2. 反向传播中梯度的计算

在单层神经网络中，反向传播的梯度为：

\[\frac{\partial L}{\partial W} = \delta \cdot \sigma'(x)\]

当导数接近 0 时：

\[\sigma'(x) \approx 0 \quad \Rightarrow \quad \frac{\partial L}{\partial W} \approx 0\]

即梯度几乎为 0，前层权重几乎不更新。

3. 多层网络中的梯度消失

深度网络中，梯度通过链式法则向前传播：

\[\frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial W_L} \cdot \prod_{i=2}^{L} \frac{\partial h_i}{\partial h_{i-1}}\]

如果每一层的激活函数导数都小于 1，例如 sigmoid 导数最大只有 0.25：

\[\prod_{i=2}^{L} \frac{\partial h_i}{\partial h_{i-1}} \to 0 \quad \text{（层数越多衰减越严重）}\]
4. 结论

梯度消失导致：

  • 靠近输入层的参数几乎无法更新
  • 深层网络难以训练
  • 长距离依赖难以学习（RNN 中尤为严重）

4、神经网络是更宽好还是更深好？

更深网络（Deep Network）更好

优点
  1. 表达能力强
    • 多层堆叠可以表示更复杂、更抽象的函数
    • 理论上，深层网络能用更少的参数逼近复杂函数（如卷积网络、ResNet）
  2. 特征分层抽象
    • 低层提取简单特征（边缘、角点）
    • 高层提取复杂结构（物体、语义）
  3. 现代深度网络效果好
    • ResNet、VGG、Transformer 都依赖深度堆叠
缺点
  • 容易梯度消失 / 梯度爆炸 → 训练困难
  • 训练速度慢，参数多 → 需要 GPU + 大数据
  • 可能过拟合（需正则化）
维度 更深网络 更宽网络
表达能力 高（分层抽象） 中等（需非常宽才能逼近深网络）
训练难度 高（梯度消失/爆炸） 低
参数效率 高（少量参数即可表达复杂函数） 低（参数量大）
适用场景 大数据 + 复杂任务（CV/NLP） 小数据或浅层任务

5、为什么要使⽤Softmax?

1. Softmax 的定义

解决这个问题首先我们得要先认识什么是Softmax

对于一个包含 $K$ 个类别的输出向量 $\mathbf{z} = [z_1, z_2, \dots, z_K]$，Softmax 的计算公式为：

\[\text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}, \quad i=1,2,\dots,K\]

其中：

  • $e^{z_i}$ 将输出映射为正数；
  • 除以所有类别的指数和，使得 输出和为 1。

用通俗的话讲就是，进行Softmax处理之后，神经网络中，对应不同神经元（可能代表着不同分类类别的预测目标）所带有的数值不再是无规律的，而是统一化的。 例如原本可能分别带有的数值是25 36 39，而在经过Softmax处理之后，变为了0.25 0.36 0.39，对应成为了预测特征属性出现的概率。

2. 使用 Softmax 的原因

  1. 将输出转换为概率
    • 相较于数据，概率更加直观地表示了预测的可能性。
  2. 便于分类决策
    • 直接取概率最大的类别即可
  3. 配合交叉熵损失函数
    • Softmax 与交叉熵（Cross-Entropy）结合，衡量预测概率分布和真实分布的差距，指导模型训练。

6、SGD 和 Adam 哪个更有效？

1. SGD Adam 分别是什么

1. SGD（Stochastic Gradient Descent）

每次用一个小批量（mini-batch）样本计算梯度，然后沿负梯度方向更新参数。

\[\theta_{t+1} = \theta_t - \eta \nabla_\theta L(\theta_t)\]

其中 $\eta$ 是学习率。

2. Adam（Adaptive Moment Estimation）

结合动量法和 RMSProp，自适应调整每个参数的学习率。

\[m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla_\theta L(\theta_t)\] \[v_t = \beta_2 v_{t-1} + (1-\beta_2) (\nabla_\theta L(\theta_t))^2\] \[\theta_{t+1} = \theta_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}\]

其中 $\hat{m}_t, \hat{v}_t$ 是偏差校正后的动量。

3. 两者比较
特性 SGD Adam
收敛速度 较慢 快
泛化能力 高 中等/有时偏低
对学习率敏感 高 低
适用场景 CNN、图像任务 NLP、Transformer、稀疏梯度问题

Adam是对于SGD的一种优化，在大部分情况下，Adam比SGD更有效

You May Also Enjoy

Quote

less than 1 minute read